Các câu hỏi tương tự
Cho hình chữ nhật ABCD, M là một điểm bất kì nằm trong hình chữ nhật đó. Chứng minh MA + MC + MB + MD < AB+AD+AC.
cho M là 1 điểm nằm trong hình chữ nhật ABCD. Gỉa sử MA=3; MB=2; MC=1. Tính MD
cho M là một điểm ở bên trong hình chữ nhật ABCD . Biết MA = 3 , MB = 2 , MC = 1 . Tính MD
Cho M là một điểm ở bên trong của hình chữ nhật ABCD. Giả sử MA = 3 ; MB = 2 ; MC = 1. Tính MD.
bài 1 cho M là một điểm ở bên trong hình chữ nhật ABCD . Biết MA = 3 , MB = 2 , MC = 1 . Tính MD
1. Cho hình chữ nhật ABCD có AD2cm; AB4cm. Kẻ đường thẳng qua C vuông góc với AC cắt các đường thẳng AB, DB lần lượt tại E và F.a) Tính độ dài BE và DFb) Gọi M là điểm di chuyển trên cạnh AB( M khác B và B). Gọi S1,S2 là diện tích ∆MCE, ∆MAM. Tìm vị trí điểm M trên AB để S13/2 S22. Cho hình vuông ABCS có cạnh bằng 1. M là điểm bất kì nằm trong hình vuông. Cm MA^2 +MB^2+MC^2+MD^2 2
Đọc tiếp
1. Cho hình chữ nhật ABCD có AD=2cm; AB=4cm. Kẻ đường thẳng qua C vuông góc với AC cắt các đường thẳng AB, DB lần lượt tại E và F.
a) Tính độ dài BE và DF
b) Gọi M là điểm di chuyển trên cạnh AB( M khác B và B). Gọi S1,S2 là diện tích ∆MCE, ∆MAM. Tìm vị trí điểm M trên AB để S1=3/2 S2
2. Cho hình vuông ABCS có cạnh bằng 1. M là điểm bất kì nằm trong hình vuông. Cm MA^2 +MB^2+MC^2+MD^2 >=2
Cho hình chữ nhật ABCD.M là một điểm bất kì trong hình chữ nhật chứng minh đẳng thức sau trong 2 TH :
\(MA^2+MC^2=MB^2+MD^2\)
\(TH1:M\in ABCD\)
\(TH2:M\notin ABCD\)
Cho hình chữ nhật ABCD. Lấy M nằm trong hình chữ nhật ABCD. Giả sử MA = 3, MB = 2, MC = 1.
Khi đó, MD^2=
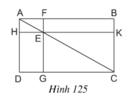
Cho hình 125 trong đó ABCD là hình chữ nhật, E là một điểm bất kì nằm trên đường chéo AC, FG // AD và HK // AB. Chứng minh rằng hai hình chữ nhật EFBK và EGDH có cùng diện tích.