Trong mp(SDC) gọi MN\(\cap\)CD=K
⇒(OMN)
Trong mp(ABCD) gọi AC ⇒(OMN)
Ta có (OMN)
(OMN)
(OMN)
(OMN)
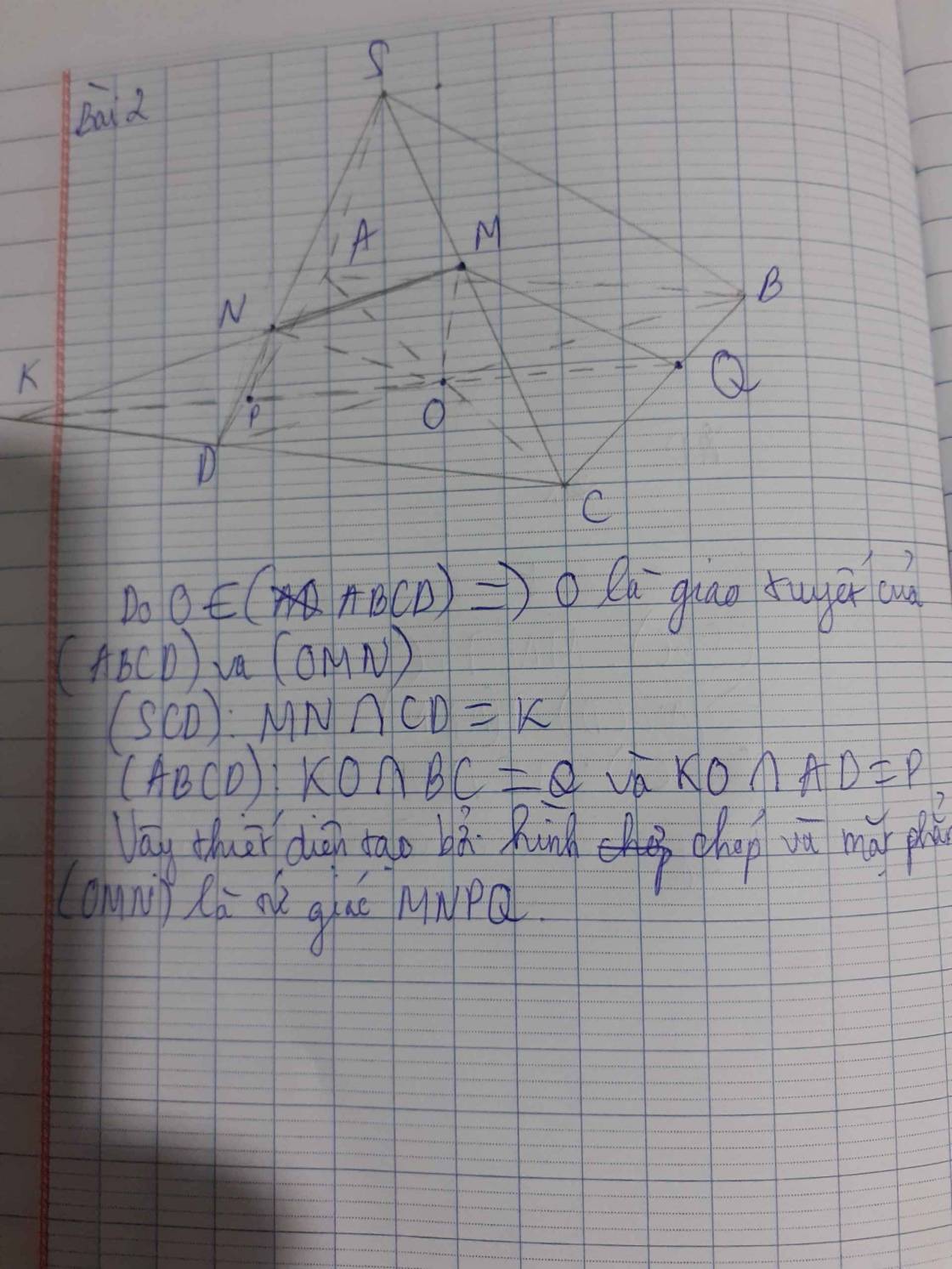
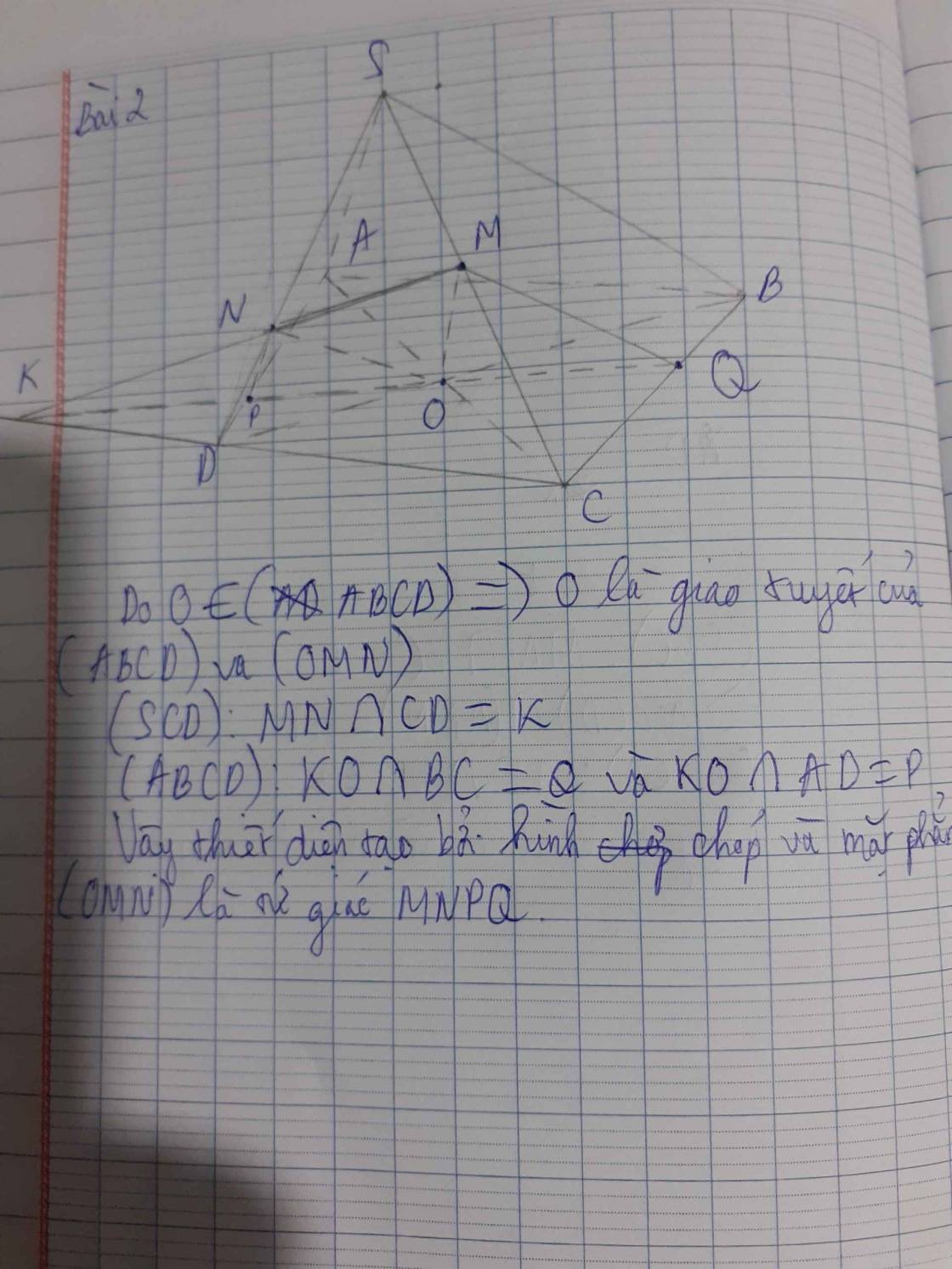
Do O (ABCD), nên ta tìm giao tuyến của (OMN) và (ABCD) trước.
Trong (SDC) : MN CD = K
Trong (ABCD):
KO AC = P
KO BD = Q
Vậy thiết diện tạo bởi hình chóp S.ABCD và mặt phẳng (OMN) là tứ giác MNPQ.
Do O (ABCD), nên ta tìm giao tuyến của (OMN) và (ABCD) trước.
Trong (SDC) : MN CD = K
Trong (ABCD):
KO AC = P
KO BD = Q
Vậy thiết diện tạo bởi hình chóp S.ABCD và mặt phẳng (OMN) là tứ giác MNPQ.
Do O (ABCD), nên ta tìm giao tuyến của (OMN) và (ABCD) trước.
Trong (SDC) : MN CD = K
Trong (ABCD):
KO AC = P
KO BD = Q
Vậy thiết diện tạo bởi hình chóp S.ABCD và mặt phẳng (OMN) là tứ giác MNPQ
Do O (ABCD), nên ta tìm giao tuyến của (OMN) và (ABCD) trước.
Trong (SDC) : MN CD = K
Trong (ABCD):
KO AC = P
KO BD = Q
Vậy thiết diện tạo bởi hình chóp S.ABCD và mặt phẳng (OMN) là tứ giác MNPQ.
Do O (ABCD), nên ta tìm giao tuyến của (OMN) và (ABCD) trước.
Trong (SDC) : MN CD = K
Trong (ABCD):
KO AC = P
KO BD = Q
Vậy thiết diện tạo bởi hình chóp S.ABCD và mặt phẳng (OMN) là tứ giác MNPQ.
Do O (ABCD), nên ta tìm giao tuyến của (OMN) và (ABCD) trước.
Trong (SDC) : MN CD = K
Trong (ABCD):
KO AC = P
KO BD = Q
Vậy thiết diện tạo bởi hình chóp S.ABCD và mặt phẳng (OMN) là tứ giác MNPQ.
Do O (ABCD), nên ta tìm giao tuyến của (OMN) và (ABCD) trước.
Trong (SDC) : MN CD = K
Trong (ABCD):
KO AC = P
KO BD = Q
Vậy thiết diện tạo bởi hình chóp S.ABCD và mặt phẳng (OMN) là tứ giác MNPQ.
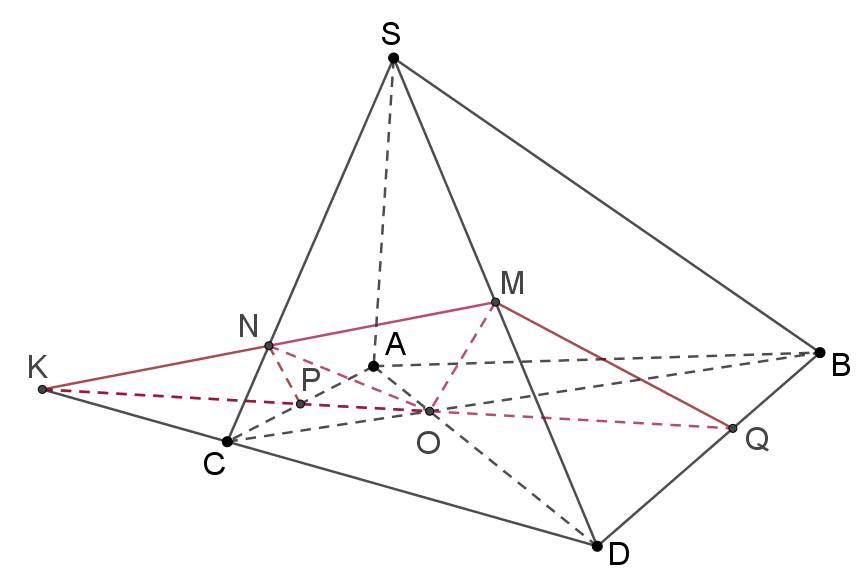
Do O ∈ (ABCD), nên ta tìm giao tuyến của (OMN) và (ABCD) trước.
Trong (SDC) : MN ∩ CD = K
Trong (ABCD):
KO ∩ AC = P
KO ∩ BD = Q
Trong (ABCD):
KO ∩ AC = P
KO ∩ BD = Q
Vậy thiết diện tạo bởi hình chóp S.ABCD và mặt phẳng (OMN) là tứ giác MNPQ
Trong mp(SDC) gọi MN ∩ CD=K
⇒(OMN) ∩ (ABCD) = OK
Trong mp(ABCD) gọi AC ∩ OK = P
⇒(OMN) ∩ (ABCD) = QP gọi KO ∩ BD = Q
Ta có :
(OMN) ∩ (SCD) = MN
(OMN) ∩ (SAC) = NP
(OMN) ∩ (ABCD) = PQ
(OMN) ∩ (SBD) = QM
Vậy thiêt diện là MNPQ
Do O (ABCD), nên ta tìm giao tuyến của (OMN) và (ABCD) trước.
Trong (SDC) : MN CD = K
Trong (ABCD):
KO AC = P
KO BD = Q
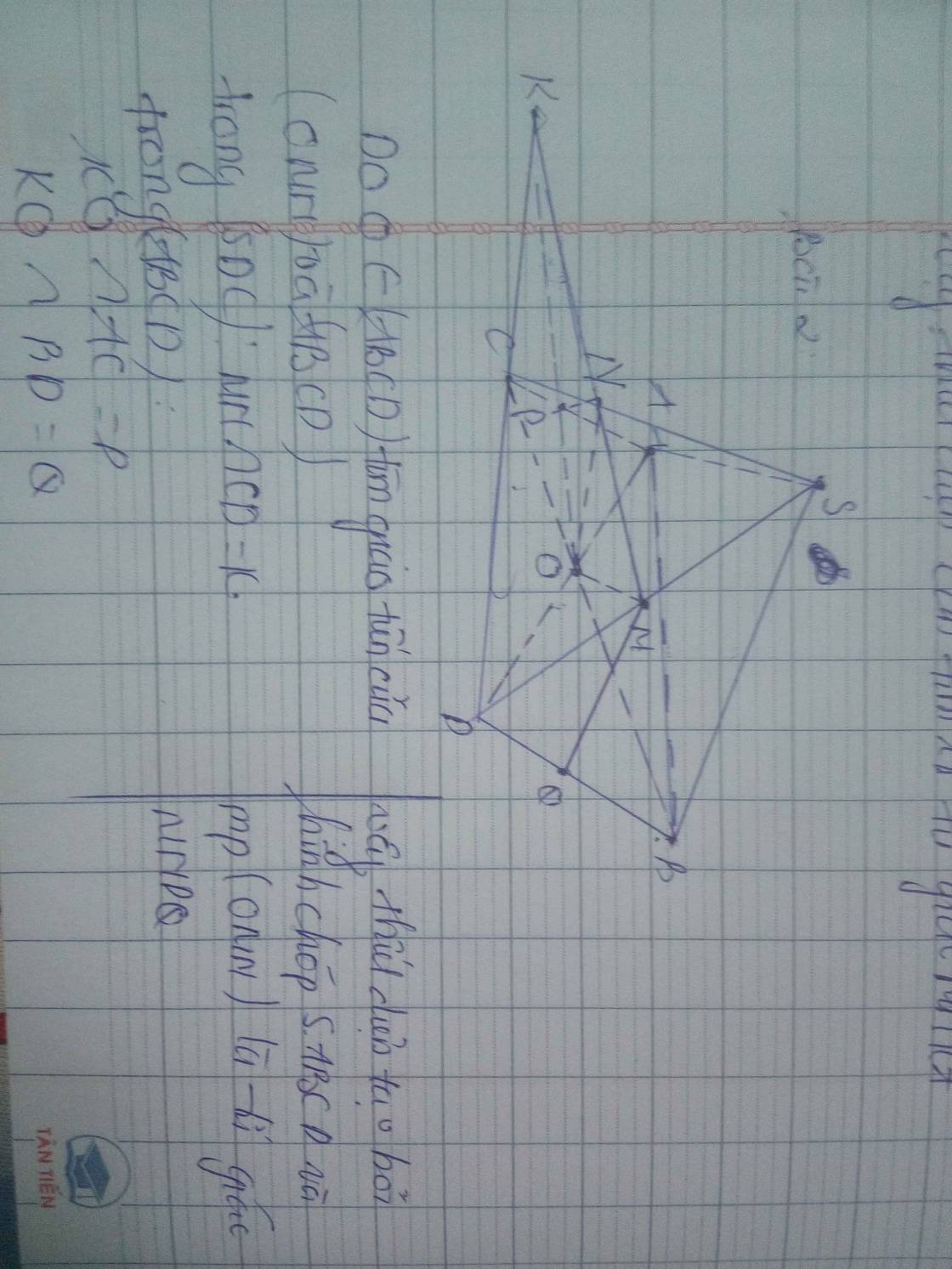
Do O thuộc (ABCD), nên ta tìm giáo tuyến của (OMN) và (ABCD) trước
Trong (ABCD):
KO là con của AC=P
KO là con của BD=Q
Vậy thiết diện tạo bởi hình chóp S.ABCD và mặt phẳng (OMN) là tứ giác MNPQ
Do O thuộc (ABCD), nên ta tìm giáo tuyến của (OMN) và (ABCD) trước
Trong (ABCD):
KO là con của AC=P
KO là con của BD=Q
Vậy thiết diện tạo bởi hình chóp S.ABCD và mặt phẳng (OMN) là tứ giác MNPQ
Do O thuộc (ABCD), nên ta tìm giáo tuyến của (OMN) và (ABCD) trước
Trong (ABCD):
KO là con của AC=P
KO là con của BD=Q
Vậy thiết diện tạo bởi hình chóp S.ABCD và mặt phẳng (OMN) là tứ giác MNPQ
Do O thuộc (ABCD), nên ta tìm giáo tuyến của (OMN) và (ABCD) trước
Trong (ABCD):
KO là con của AC=P
KO là con của BD=Q
Vậy thiết diện tạo bởi hình chóp S.ABCD và mặt phẳng (OMN) là tứ giác MNPQ
Trong (SBC):MN là con của BC=E.
Vậy (ABCD) là con của (AMN)=AE
Trong (ABCD):AE là con của CD=K
Vậy thiết diện cần tìm là tứ giác MNKA
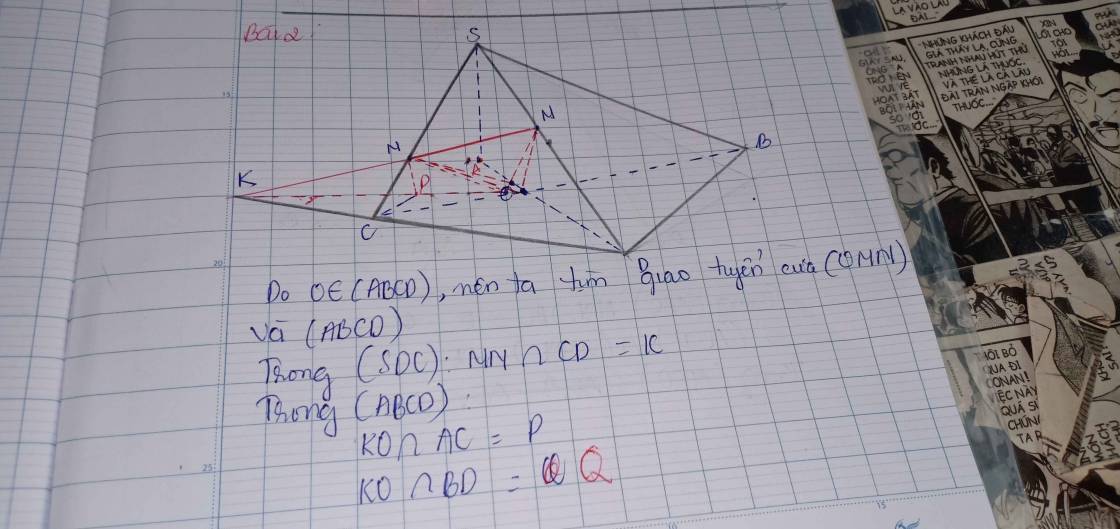
Ta có: O là điểm chung của (OMN) và (ABCD)
Trong (SCD): gọi MN giao CD tại K
Trong (ABCD): gọi KO giao AC tại P ; KO giao BD tại Q
Vậy thiết diện tạo bởi hình chóp và (OMN) là MNPQ
Do O (ABCD), nên ta tìm giao tuyến của (OMN) và (ABCD) trước.
Trong (SDC) : MN CD = K
Trong (ABCD):
KO AC = P
KO BD = Q
Vậy thiết diện tạo bởi hình chóp S.ABCD và mặt phẳng (OMN) là tứ giác MNPQ.