\(\left\{{}\begin{matrix}CD\perp AD\left(gt\right)\\SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\end{matrix}\right.\)
\(\Rightarrow CD\perp\left(SAD\right)\Rightarrow CD\perp SD\)
\(\Rightarrow\Delta SCD\) vuông tại D
\(\left\{{}\begin{matrix}CD\perp AD\left(gt\right)\\SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\end{matrix}\right.\)
\(\Rightarrow CD\perp\left(SAD\right)\Rightarrow CD\perp SD\)
\(\Rightarrow\Delta SCD\) vuông tại D
Cho hình chóp S.ABCD có đáy là hình bình hành tâm O, SA=SC, SB=SD. Trong các khẳng định sau, khẳng định nào đúng ?
A. S A ⊥ ( A B C D )
B. S O ⊥ ( A B C D )
C. S C ⊥ ( A B C D )
D. S B ⊥ ( A B C D )
Cho hình chóp S.ABCD có SA vuông góc với mặt phẳng (ABC), đáy ABC là tam giác cân tại A và B A C ^ = 120 ∘ , B C = 2a. Gọi M, N lần lượt là hình chiếu của điểm A trên SB, SC. Tính bán kính mặt cầu đi qua bốn điểm A, N, M, B.
![]()
![]()
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a (a > 0). Hai mặt phẳng (SBC) và (SCD) cùng tạo với mặt phẳng (ABCD) một góc 45 ∘ . Biết SB = a và hình chiếu của S trên mặt phẳng (ABCD) nằm trong hình vuông ABCD. Tính thể tích khối chóp S.ABCD


Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng 1, mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính thể tích V của khối cầu ngoại tiếp hình chóp đã cho.
A. 5 π 15 18
B. 5 π 15 54
C. 4 π 3 27
D. 5 π 3
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với mặt đáy và SA = a. Tính diện tích mặt cầu ngoại tiếp hình chóp S.ABC.
A. 3 πa 2 7
B. 7 πa 2 12
C. 7 πa 2 3
D. πa 2 7
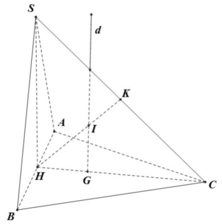
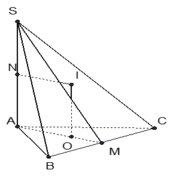
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2 2 , cạnh bên SA vuông góc với mặt phẳng đáy và SA = 3. Mặt phẳng ( α ) qua A và vuông góc với SC cắt các cạnh SB, SC, SD lần lượt tại các điểm M, N, P. Tính thể tích V của khối cầu ngoại tiếp tự diện CMNP.
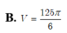


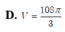
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2 2 , cạnh bên SA vuông góc với mặt phẳng đáy và SA = 3. Mặt phẳng ( α ) qua A và vuông góc với SC cắt các cạnh SB, SC, SD lần lượt tại các điểm M, N, P. Tính thể tích V của khối cầu ngoại tiếp tự diện CMNP.
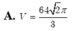
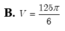
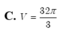
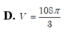
Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông tại A có BC = 2a. Biết góc giữa hai mặt phẳng (A'BC) và (ABC) bằng 60 ∘ và khoảng cách giữa hai đường thẳng A'A, BC bằng a 3 2 . Tính thể tích lăng trụ ABC.A'B'C'
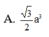
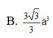
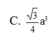
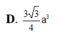
Cho hình chóp S. ABC có đáy là tam giác ABC đều cạnh a, tam giác SBA vuông tại B, tam giác SAC vuông tại C. Biết góc giữa hai mặt phẳng (SAB) và (ABC) bằng 60 o . Tính thể tích khối chóp S.ABC theo a.
A. 3 a 3 8
B. 3 a 3 12
C. 3 a 3 6
D. 3 a 3 4