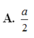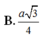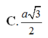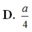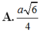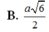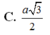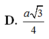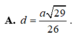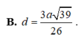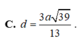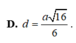Cho hình chóp S.ABCD có đáy là hình thoi tâm với BAD = 1200 và BD = a. Cạnh bên SA vuông góc với đáy. Góc giữa mặt (SBC) và đáy bằng 600. Mặt phẳng (P) đi qua BD và vuông góc với cạnh SC. Tính tỉ số thể tích giữa hai phần của hình chóp do mặt phẳng (P) tạo ra khi cắt hình chóp?

A. 10
B. 11
C. 12
D. 13
Đáp án D
Từ O kẻ OH vuông góc với SC, ta có S C ⊥ ( B D H )
Ta có V S . A H D V S . A C D = S H S C , V S . A H B V S . A C B = S H S C
mà V S . A C D = V S . A C B = 1 2 V S . A B C D = V 2
nên V S . A H D + V S . A H B V 2 = 2 S H S C
⇔ V S . A B H D V = S H S C
Có
B
C
⊥
(
S
A
M
)
nên
![]()
⇒ S A = 3 a 2
Mặt khác: ∆ C A S ~ ∆ C H O
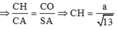
Suy ra S H S C = S C - H C S C = 1 - H C S C = 11 13
⇒ V S . A B H D = 11 13 V
Do đó
V H . B C D = V - V S . A B H D = V = 11 12 V = 2 13 V