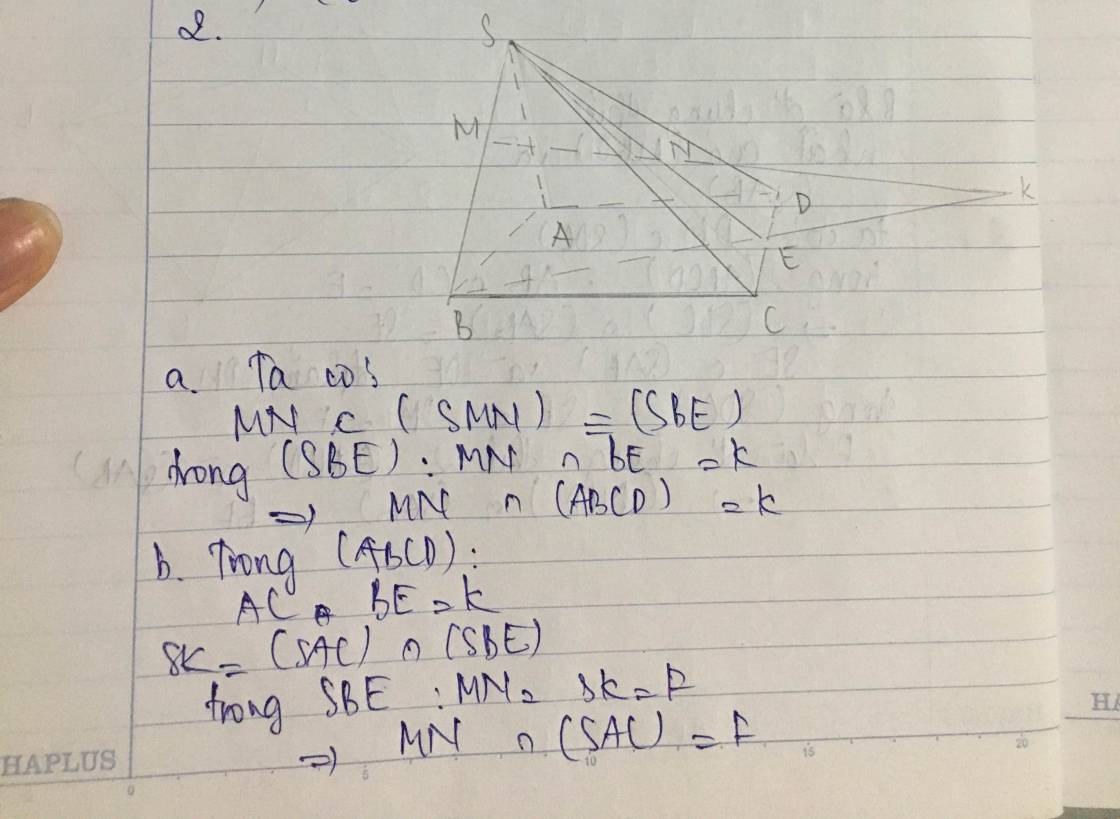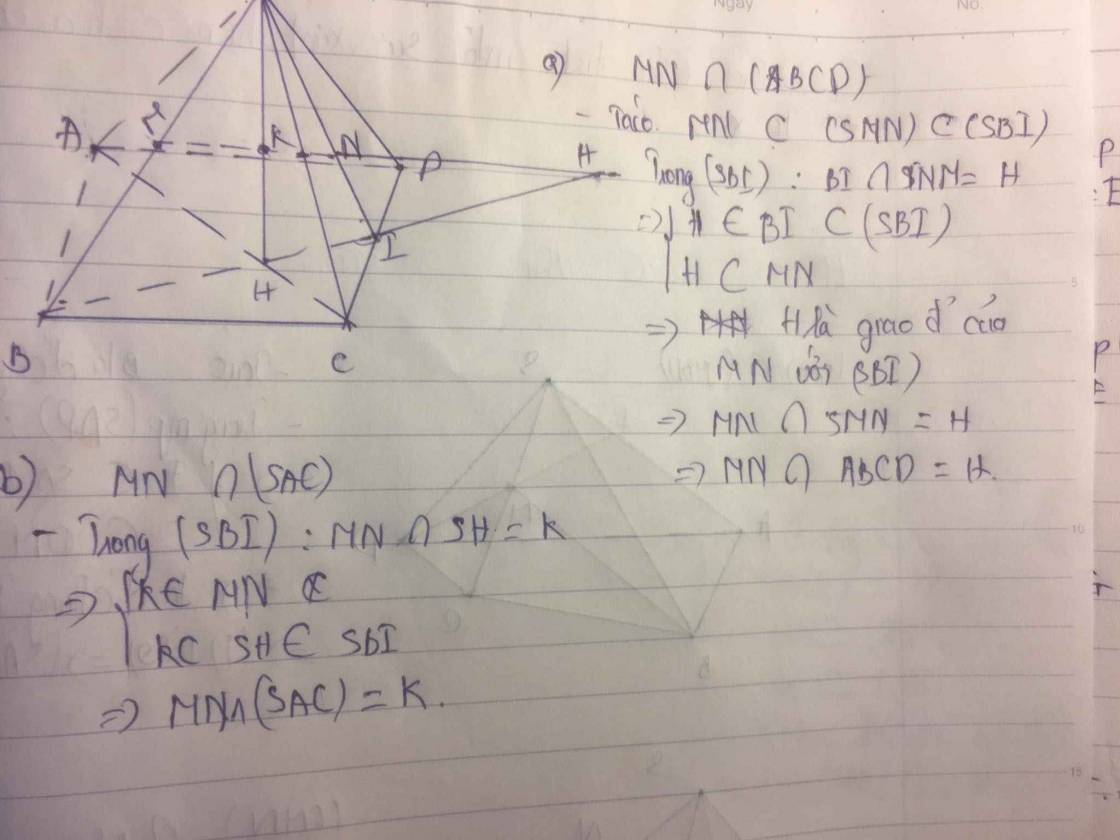Question

Cho hình chóp S.ABCD có đáy là hình bình hành. M là trung điểm SB; N là trọng tâm tam giác SCD.Tìm giao điểm của:

a. MN với (ABCD);

b. MN với (SAC).

Answer 1

a. Ta có MN \(\subset\)(SMN) \(\equiv\)(SBE)

Trong (SBE): MN \(\cap\)BE = K. Vậy MN \(\cap\)(ABCD) =K

b. Trong (ABCD): AC \(\cap\)BE = K

SK = (SAC)\(\cap\)(SBE).

Trong (SBE): MN \(\cap\) SK = F

Vậy MN \(\cap\) (SAC) = F.

Answer 2

Answer 3

a. Có MN ⊂ (SMN) ≡ (SBE) 

Trong (SBE) có MN và BE cắt tại T 

Vậy T là giao điểm của MN và (ABCD)

b. Trong (ABCD) có AC cắt BE rại L 

SL = (SAC) và (SBE) 

Trong(SBE) có MN cắt SL tại Q 

Vậy Q là giao điểm của MN và (SAC)

Answer 4

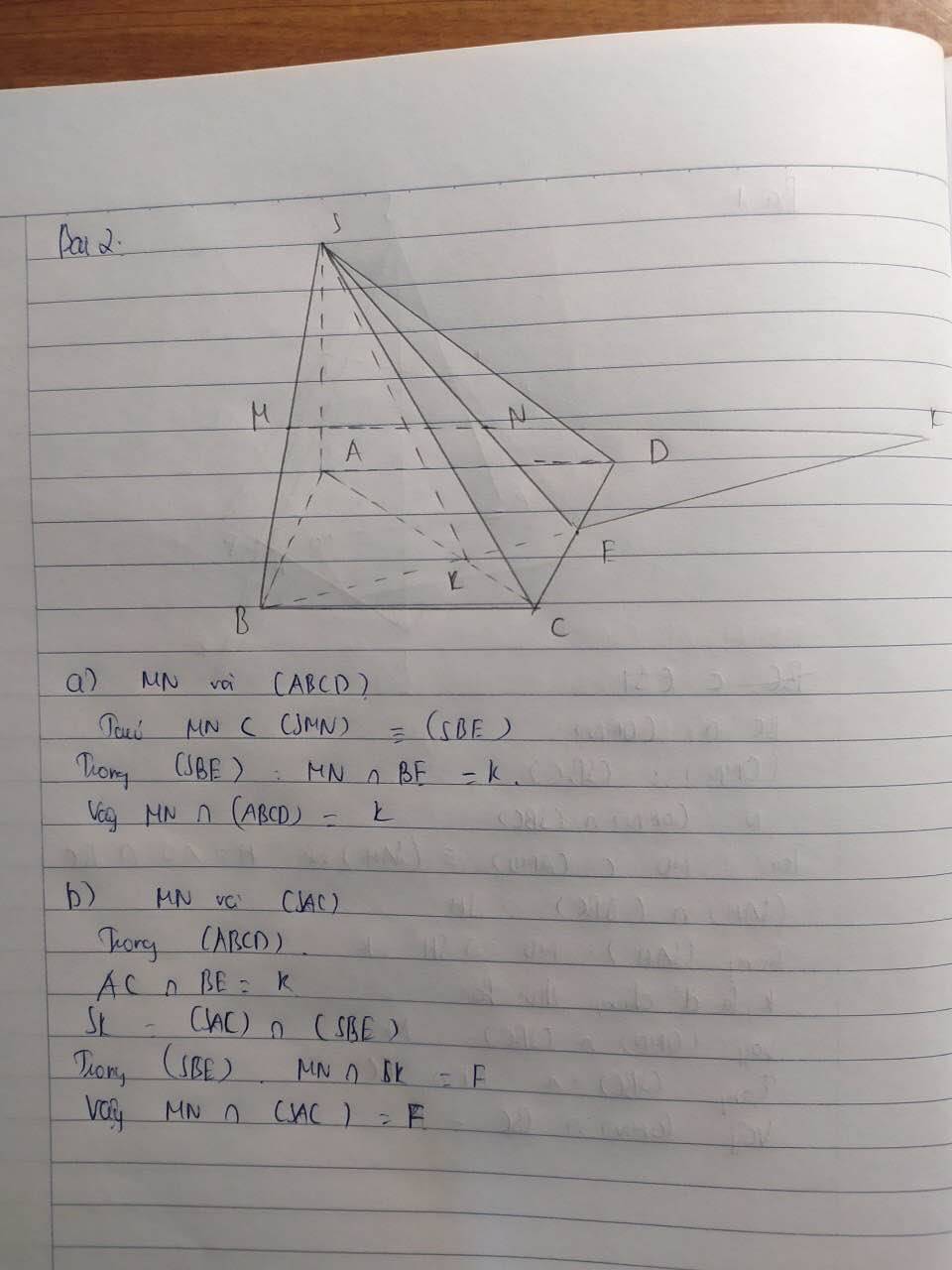
a, Ta có MN nằm trong (SMN) trùng (SBE).

Trong (SBE): MN cắt BE = k. Vậy MN cắt (ABCD) = K

b, Trong (ABCD): AC cắt BE = K

SK = (SAC) cắt (SBE).

Trong (SBE): MN cắt SK = F

Vậy MN cắt (SAC) = F

Answer 5

a. Có MN ⊂ (SMN) ≡ (SBE) Trong (SBE) có MN và BE cắt tại T Vậy T là giao điểm của MN và (ABCD) b. Trong (ABCD) có AC cắt BE rại L SL = (SAC) và (SBE) Trong(SBE) có MN cắt SL tại Q Vậy Q là giao điểm của MN và (SAC)

Answer 6

  

Answer 7

A) Giao điểm của MN với (ABCD) là K

B) giao điểm của MN với (SAC) là F

Answer 8

  

Answer 9

a) Ta có MN $\subset$ (SMN) $\equiv$ (SBE).

Trong (SBE): MN $\cap$ BE = K.

Vậy MN $\cap$ (ABCD) = K

b) Trong (ABCD): AC $\cap$ BE = K

SK=(SAC)$\cap$(SBE). 

Trong (SBE): MN $\cap$ SK = F

Vậy MN $\cap$ (SAC) = F.

Answer 10

a. Ta có MN $\subset$ (SMN) $\equiv$ (SBE).

Trong (SBE): MN $\cap$ BE =K. Vậy MN $\cap$ (ABCD) =K

b. Trong (ABCD): AC $\cap$ BE = K

SK=(SAC)$\cap$(SBE). 

Trong (SBE): MN $\cap$ SK = F

Vậy MN $\cap$ (SAC) = F.

Answer 11

Câu a:  Gọi giao điểm SN với CD là E , có BE thuộc (ABCD) mà BE cắt MN trong (SBE) tại G vậy suy ra G là giao điểm của MN và (ABCD)                          Câu b : có BE cắt AC tại O trong (ABCD), trong (SBE) SO cắt MN tại F , suy ra F là giao điểm của MN với (SAC)

Answer 12

 

Answer 13

k=MN cắt (ABCD)

f=MN cắt (SAC)

Answer 14

a) Ta có: SN cắt CD tại I 

               MN ⊂ (SBI)  

Nối MN giao BI tại Q 

     BI ⊂ (ABCD) 

=> Q là giao điểm MN với (ABCD) 

 

Answer 15

a. Ta có MN $\subset$ (SMN) $\equiv$ (SBE).

Trong (SBE): MN $\cap$ BE =K. Vậy MN $\cap$ (ABCD) =K

b. Trong (ABCD): AC $\cap$ BE = K

SK=(SAC)$\cap$(SBE). 

Trong (SBE): MN $\cap$ SK = F

Vậy MN $\cap$ (SAC) = F.

 

Answer 16

a. Có MN ⊂ (SMN) ≡ (SBE)

Trong (SBE) có MN và BE cắt tại T

Vậy T là giao điểm của MN và (ABCD)

b. Trong (ABCD) có AC cắt BE tai L

SL = (SAC) và (SBE)

Trong(SBE) có MN cắt SL tại Q

Vậy Q là giao điểm của MN và (SAC)

Answer 17

 

Answer 18

Answer 19

a. Có MN ⊂ (SMN) ≡ (SBE)

 Trong (SBE) có MN và BE cắt tại T

 Vậy T là giao điểm của MN và (ABCD)

 b. Trong (ABCD) có AC cắt BE rại L

 SL = (SAC) và (SBE)

 Trong(SBE) có MN cắt SL tại Q

 Vậy Q là giao điểm của MN và (SAC)

Answer 20

a. Ta có MN $\subset$ (SMN) $\equiv$ (SBE).

Trong (SBE): MN $\cap$ BE =K. Vậy MN $\cap$ (ABCD) =K

b. Trong (ABCD): AC $\cap$ BE = K

SK=(SAC)$\cap$(SBE). 

Trong (SBE): MN $\cap$ SK = F

Vậy MN $\cap$ (SAC) = F.

 

Answer 21

a. Ta có MN $\subset$ (SMN) $\equiv$ (SBE).

Trong (SBE): MN $\cap$ BE =K. Vậy MN $\cap$ (ABCD) =K

b. Trong (ABCD): AC $\cap$ BE = K

SK=(SAC)$\cap$(SBE). 

Trong (SBE): MN $\cap$ SK = F

Vậy MN $\cap$ (SAC) = F.

 

 

Answer 22

a. Ta có MN $\subset$ (SMN) $\equiv$ (SBE).

Trong (SBE): MN $\cap$ BE =K. Vậy MN $\cap$ (ABCD) =K

b. Trong (ABCD): AC $\cap$ BE = K

SK=(SAC)$\cap$(SBE). 

Trong (SBE): MN $\cap$ SK = F

Vậy MN $\cap$ (SAC) = F.

Answer 23

  

Answer 24

 

 

Answer 25

  

Answer 26

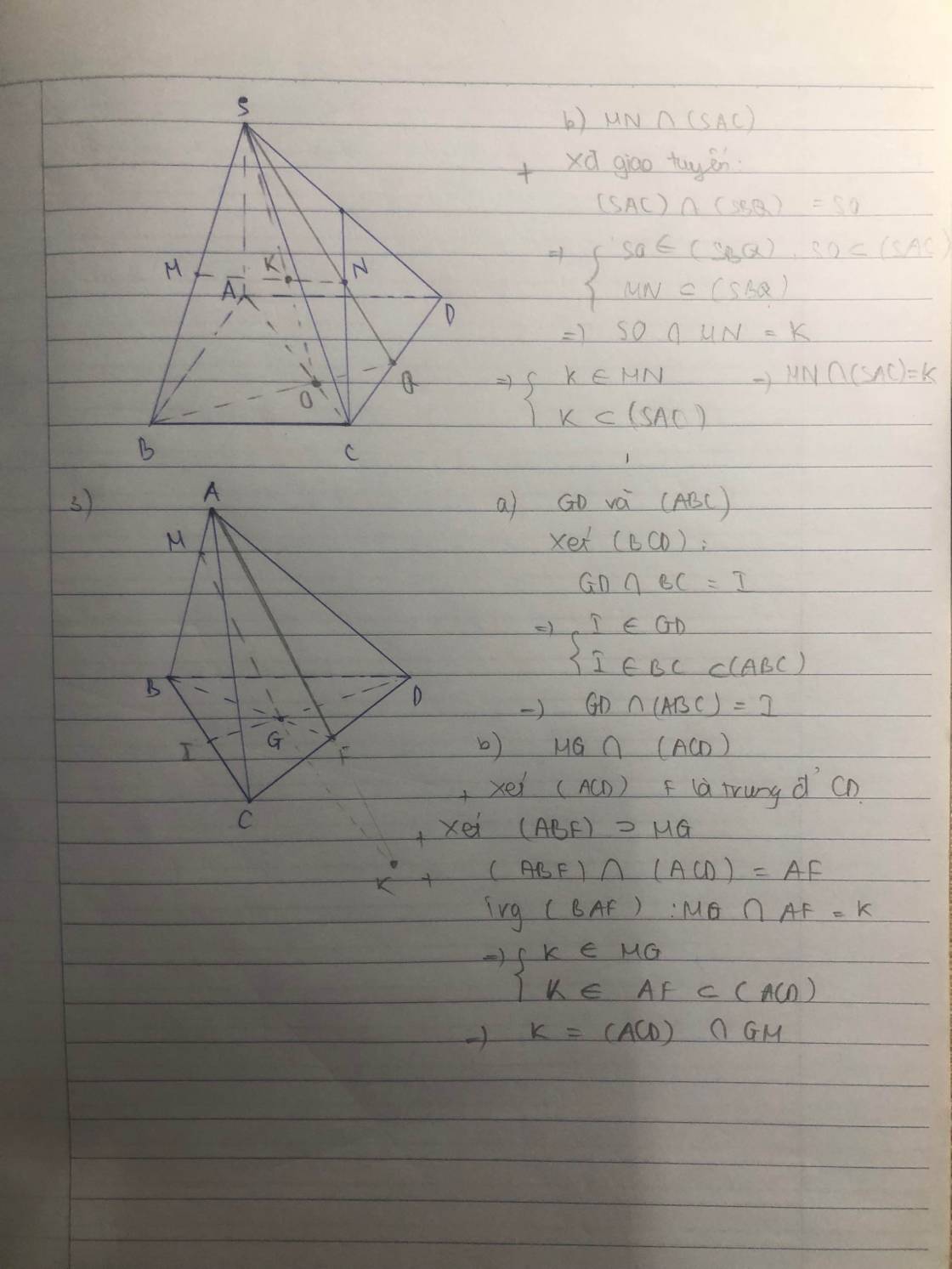
a, gọi E là tdiem CD .trong mp(SBD) gọi F=MN GIAO BE=> F€MN , F€BE nằm trong ( ABCD)=>F=MN GIAO (ABCD)       b, chọn mp (SBE) chứa MN .tìm giao tuyến (SBE)va(SAC) có S thuộc (SAC) giao)SBE) (1) trong mp(ABCD) gọi G=AC giaoBE=> G thuộc AC giao(SAC) . G thuộc BE nằm trong (SBE) =>G thuộc(SAC) giao (SBE) (2) từ 1và2 =>(SAC) giao(SBE) tạu SG . trong mp (SBE) gọi H =MN giAO SG=>H thuộc MN . H thuộc SG nằm trong (SAC) =>H=MN giao (SAC)

 

Answer 27

Answer 28

Answer 29

a) Gọi ae là TĐ của CD 

trong mp <SBE> gọi 

F= MN giao BE => { F ϵ MN

                               { F ϵ BE ⊂ABCD 

=> F= MN giao (ABCD) 

b)  có S ϵ (SAC) giao (SBE) (1) 

trong mp (ABCD) gọi 

G= AC giao BE => G ϵ AC ⊂(SAC) 

G ϵ BE ⊂( SBE) 

= ) G ϵ (SAC) giao (SBE) (2) 

(1)(2) =) (SAC ) Giao (SBE) = SG 

trong mp (SBE) gọi H = MN giao SG => H ϵ MN , H ϵSG ⊂(SAC) 

=) h= MM gió (SAC) 

Answer 30

a. Có MN ⊂ (SMN) ≡ (SBE) 

Trong (SBE) có MN và BE cắt tại T 

Vậy T là giao điểm của MN và (ABCD)

b. Trong (ABCD) có AC cắt BE rại L 

SL = (SAC) và (SBE) 

Trong(SBE) có MN cắt SL tại Q 

Vậy Q là giao điểm của MN và (SAC)