Question

Cho hình chóp s.abcd có đáy là hình bình hành .gọi M là trung điểm SD a, tìm giao điểm I của BM và SAC . tính IB/IM b, tìm giao điểm J của SA và BCM . Tính JS/JA E cần gấp ạ giúp e vứiiii huhu

Answer 1

Answer 2

Theo định lý Menelaus, ta có:

\(\dfrac{JS}{JA}.\dfrac{CA}{CO}.\dfrac{IO}{IS}=1\Rightarrow\dfrac{JS}{JA}=1\)

Answer 3

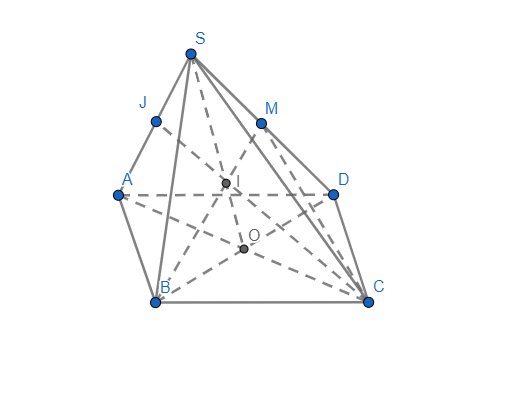
Trong mp(ABCD), gọi \(O=AC\cap BD\)

a) Ta có:

\(\left\{{}\begin{matrix}S\in\left(SAC\right)\\S\in\left(SBD\right)\end{matrix}\right.\)\(\Rightarrow S\in\left(SAC\right)\cap\left(SBD\right)\)

\(\left\{{}\begin{matrix}O\in BD\subset\left(SBD\right)\\O\in AC\subset\left(SAC\right)\end{matrix}\right.\)\(\Rightarrow O\in\left(SAC\right)\cap\left(SBD\right)\)

\(\Rightarrow SO=\left(SAC\right)\cap\left(SBD\right)\)

Trong mp(SBD), gọi \(I=SO\cap BM\Rightarrow I=BM\cap\left(SAC\right)\)

Ta có: \(\left\{{}\begin{matrix}SM=DM\\OB=OD\end{matrix}\right.\)\(\Rightarrow\dfrac{IB}{IM}=2\)

b) Ta có:

\(\left\{{}\begin{matrix}I\in SO\subset\left(SAC\right)\\I\in BM\subset\left(MBC\right)\end{matrix}\right.\)\(\Rightarrow I\in\left(SAC\right)\cap\left(MBC\right)\)

\(\left\{{}\begin{matrix}C\in\left(SAC\right)\\C\in\left(MBC\right)\end{matrix}\right.\)\(\Rightarrow C\in\left(SAC\right)\cap\left(MBC\right)\)

\(\Rightarrow IC=\left(SAC\right)\cap\left(MBC\right)\)

Trong mp(SAC), gọi \(J=SA\cap IC\)\(\Rightarrow J=SA\cap\left(MBC\right)\)

Theo định lý Menelaus, ta có:

\(\dfrac{JS}{JA}.\dfrac{CA}{CO}.\dfrac{IO}{SO}=1\)\(\Rightarrow\dfrac{JS}{JA}.2.\dfrac{1}{3}=1\Leftrightarrow\dfrac{JS}{JA}=\dfrac{3}{2}\)