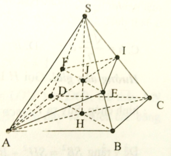
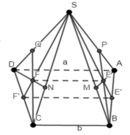
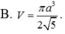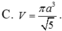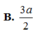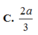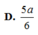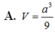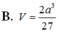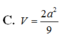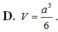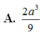Cho hình chóp S.ABCD có đáy ABCD là một hình thang với đáy AD và BC. Biết AD = a, BC = b. Gọi I và J lần lượt là trọng tâm các tam giác SAD và SBC. Mặt phẳng (ADJ) cắt SB, SC lần lượt tại M, N. Mặt phẳng (BCI) cắt SA, SD tại P, Q. Giả sử AM cắt BP tại E; CQ cắt DN tại F. Tính EF theo a,b
A. E F = 1 2 ( a + b )
B. E F = 3 5 ( a + b )
C. E F = 2 3 ( a + b )
D. E F = 2 5 ( a + b )
Đáp án D
Dễ thấy rằng:
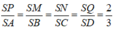
![]()
Giả sử S E ∩ A B = E ' ; S F ∩ C D = F '
Áp dụng định lý Ceva vào tam giác SAB có:

⇔ E ' A = E ' B ⇒ E ' là trung điểm của AB.
Chứng minh tương tự ta cũng có F ' là trung điểm của CD
⇒ E ' F ' là đường trung bình của hình thang ABCD
![]()
Áp dụng định lý Menelaus vào tam giác SBE’ với cát tuyến AEM có:
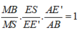
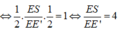
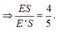
Chứng minh tương tự ta cũng có:
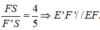
Áp dụng định lý Thales vào tam giác SE’F’ có:
![]()
![]()