Đáp án C
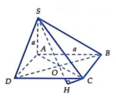
Gọi H là hình chiếu của C trên SO(O = AC ∩ BD), vì góc SOC tù nên H nằm ngoài SO
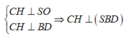
=> Góc tạo bởi SC và (SBD) là C S O ^
Ta có ![]()
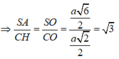
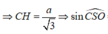
![]()
Đáp án C

Gọi H là hình chiếu của C trên SO(O = AC ∩ BD), vì góc SOC tù nên H nằm ngoài SO
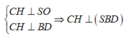
=> Góc tạo bởi SC và (SBD) là C S O ^
Ta có ![]()
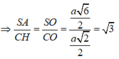
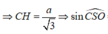
![]()
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, cạnh bên SA vuông góc với mặt phẳng đáy, SA = AB = a Tính góc giữa đường thẳng SC và mặt phẳng (SBD)
A. arcsin 1 4 B. arcsin 1 3 C. arcsin 1 3 D. arcsin 2 3
B. arcsin 1 3
C. arcsin 1 3
D. arcsin 2 3
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh a, SA vuông góc với đáy (ABCD) Góc giữa đường thẳng SC và mặt phẳng (SAB) bằng
α
với 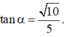 Tính góc giữa đường thẳng SO và mặt phẳng (ABCD)
Tính góc giữa đường thẳng SO và mặt phẳng (ABCD)
A. 60 o
B. 69 , 3 o
C. 90 o
D. 45 o
Hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = 1 và AD = 3 . Cạnh bên SA vuông góc với mặt phẳng đáy và SC tạo với mặt phẳng (ABCD) một góc 60 0 . Tính thể tích V của khối chóp S,ABCD
A. V = 3
B. V = 2
C. V = 6
D. V = 1
Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặt đáy và S A = a 2 . Tìm số đo của góc giữa đường thẳng SC và mặt phẳng (SAB)
A. 45 °
B. 30 °
C. 90 °
D. 60 °
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB=a, BC=a 3 Cạnh bên SA =a và vuông góc với đáy (ABCD) Cosin của góc tạo bởi giữa đường thẳng BD và mặt phẳng (SBC) bằng
A. 3 2
B. 14 4
C. 3 5
D. 22 5
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 3a, SA = a 3 vuông góc với đáy. Góc giữa đường thẳng SD và mặt phẳng (ABCD) bằng:
![]()
![]()
![]()
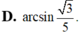
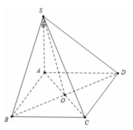
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a các mặt bên (SAB), (SAD) cùng vuông góc với mặt phẳng đáy, SA=a; góc giữa đường thẳng SC và mặt phẳng (SAB) bằng a. Khi đó tan α nhận giá trị nào trong các giá trị sau:
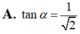
![]()
![]()
![]()
Cho hình chóp S.ABCD có đáy là hình vuông, SA vuông góc với đáy. Góc giữa đường thẳng SC và mặt phẳng (ABCD) là
![]()
![]()
![]()
![]()
Cho hình chóp S.ABCD có đáy là hình vuông, SA vuông góc với đáy. Góc giữa đường thẳng SC và mặt phẳng (ABCD) là
![]()
![]()
![]()
![]()