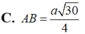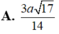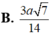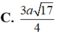Question

Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, góc ABC = 60 độ. Gọi O là giao điểm của AC và BD. Biết rằng SO vuông góc (ABCD), SO=3a/4. Khoảng cách từ O đến mặt phẳng (SCD) bằng ma/n với m/n là phân số tối giản, m>0, n>0. Giá trị m+n bằng 3+4 căn 7 là đúng hay sai

Answer 1

Kẻ OH vuông CD tại H

Ta có SO vuông CD; CD vuông OH => CD vuông (SOH) 

Từ O kẻ OK vuông SH 

Lại có CD vuông (SOH) => CD vuông OK 

=> OK là khoảng cách từ O đến (SCD) 

Xét tam giác ABC có ^ABC = 60⁰;AB=BC 

=> tam giác ABC đều => AC = a => OC = a/2 

Xét tam giác BCD có ^BCD = 120⁰

\(cos120=\dfrac{BC^2+CD^2-BD^2}{2.BC.CD}\Rightarrow BD=\sqrt{3}\)

=> OD = căn 3/2 

Xét tam giác COD vuông tại O 

ADHT \(\dfrac{1}{OH^2}=\dfrac{1}{OC^2}+\dfrac{1}{OD^2}=\dfrac{1}{a^2}+\dfrac{1}{\dfrac{3}{4}a^2}\Rightarrow OH=\sqrt{\dfrac{3}{7}}\)a

Xét tam giác SOH vuông tại O ADHT 

\(\dfrac{1}{OK^2}=\dfrac{1}{OH^2}+\dfrac{1}{SO^2}=\dfrac{1}{\dfrac{3}{7}a^2}+\dfrac{1}{\dfrac{9}{16}a^2}\Rightarrow OK=\dfrac{3}{\sqrt{37}}\)

=> m + n = \(3+\sqrt{37}\)

=> sai