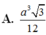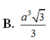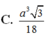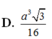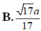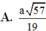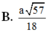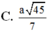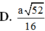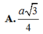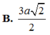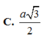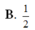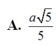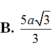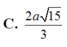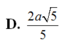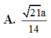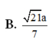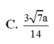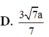Kẻ OH vuông CD
Dựng OK vuông SH
=> OK là kc (O;(SCD))
Do O, là trung điểm BD; H là trung điểm DC
Nên OH là đường tb
=> OH = BC/2 = a/2
Xét tam giác SOH vuông tại O , OK là đường cao
ADHT \(\dfrac{1}{OK^2}=\dfrac{1}{OH^2}+\dfrac{1}{SO^2}\Rightarrow OK=\dfrac{3\sqrt{13}}{26}a\)
\(m+n=3\sqrt{13}+26\)