Lời giải:
Do $SA\perp (ABCD)$ nên $\angle (SB, ABCD)=\angle (SB, AB)=\widehat{SBA}=45^0$
$\Rightarrow SAB$ là tam giác vuông cân tại $A$
$\Rightarrow SA=AB=a$
Áp dụng định lý Pitago: $SD=\sqrt{SA^2+AD^2}=\sqrt{a^2+(2a)^2}=\sqrt{5}a$
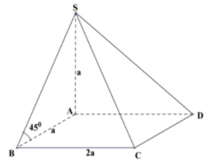
Cho hình chóp S.ABCD có đáy là hình chữ nhật, SA vuông góc với mặt đáy (ABCD), AB = a, AD = 2a. Góc giữa cạnh bên SB và mặt phẳng (ABCD) bằng 45 ° . Thể tích hình chóp S.ABCD bằng
A. 2 a 3 3
B. a 3 3
C. 6 a 3 18
D. 2 2 a 3 3
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA vuông góc với mặt đáy (ABCD), AB = a, AD = 2. Góc giữa cạnh bên SB và mặt phẳng (ABCD) bằng 45°. Thể tích hình chóp S.ABCD bằng
A. 6 a 3 18
B. 2 2 a 3 3
C. a 3 3
D. 2 a 3 3
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB=a; AD=2a, cạnh bên SA vuông góc với đáy và thể tích khối chóp S.ABCD bằng 2 a 3 3 . Tính số đo góc giữa đường thẳng SB với mặt phẳng (ABCD).
A. 30 0
B. 60 0
C. 45 0
D. 75 0
Cho hình chóp S.ABCD có đáy là hình chữ nhật AB=2a, A D = a 3 , cạnh bên SA vuông góc với mặt phẳng đáy, góc giữa đường thẳng SD và mặt phẳng đáy bằng 30 ° . Diện tích mặt cầu ngoại tiếp hình chóp là.
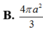
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = a, A D = a 3 , S A vuông góc với mặt phẳng (ABCD), góc giữa đường thẳng SD và mặt phẳng (ABCD) bằng 60 0 . Gọi M là trung điểm của cạnh AD. Khoảng cách giữa hai đường thẳng CM và SB bằng
Cho hình chóp S.ABCD có đáy là hình chữ nhật, AB=2a, AD=a 3 , cạnh bên SA vuông góc với mặt phẳng đáy, góc giữa SD và mặt phẳng đáy là 30 ° . Diện tích mặt cầu ngoại tiếp hình chóp là:
Cho hình chóp S.ABCD có đáy là hình chữ nhật, AB = 2a, AD = a 3 , cạnh bên SA vuông góc với mặt phẳng đáy, góc giữa SD và mặt phẳng đáy là 30o. Diện tích mặt cầu ngoại tiếp hình chóp là
A. 8 πa 2
B. 8 πa 2 3
C. 4 πa 2
D. 4 πa 2 3
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật,AB=a, AD=2a; cạnh bên SA vuông góc với mặt đáy và S A = a 5 . Khoảng cách giữa hai đường thẳng AB và SD bằng
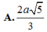
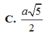
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật có A B = a , B C = 2 a và S A = S C và S B = S D . Cạnh SC tạo với mặt phẳng đáy một góc bằng 60 0 . Thể tích khối chóp S.ABCD bằng:
