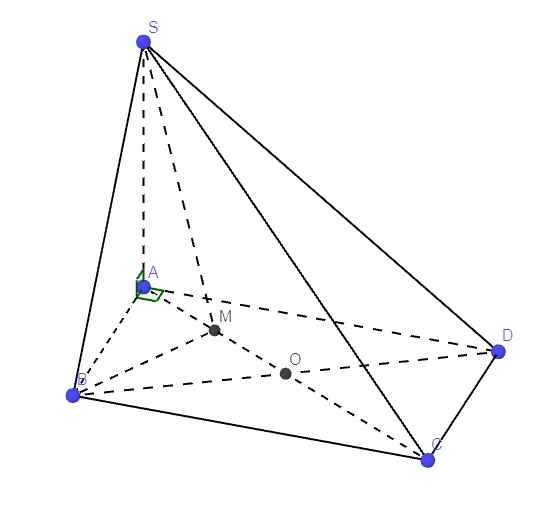
\(AC=\sqrt{AB^2+BC^2}=2a\) \(\Rightarrow AO=\dfrac{1}{2}AC=a\) ; \(AM=\dfrac{1}{2}AO=\dfrac{a}{2}\)
\(SA\perp\left(ABCD\right)\Rightarrow AC\) là hình chiếu vuông góc của SC lên (ABCD)
\(\Rightarrow\widehat{SCA}\) là góc giữa SC và (ABCD) \(\Rightarrow\widehat{SCA}=45^0\)
\(\Rightarrow SA=AC.tan45^0=2a\)
\(AB^2=a^2\) ; \(AM.AC=\dfrac{a}{2}.2a=a^2\Rightarrow AB^2=AM.AC\)
\(\Rightarrow\dfrac{AB}{AM}=\dfrac{AC}{AB}\Rightarrow\Delta ABM\sim\Delta ACB\left(c.g.c\right)\)
\(\Rightarrow\widehat{AMB}=\widehat{ABC}=90^0\Rightarrow BM\perp AC\)
Lại có \(SA\perp\left(ABCD\right)\Rightarrow SA\perp BM\)
\(\Rightarrow BM\perp\left(SAC\right)\Rightarrow\left(SBM\right)\perp\left(SAC\right)\)