Đáp án B.
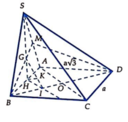
Gọi H là trung điểm AB, G là trọng tâm
Trong mặt phẳng (ABCD), ![]()
Ta có: ![]()
Gọi I là hình chiếu của H lên BD, K là hình chiếu của H lên GI
![]()
Ta có: 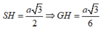
![]()
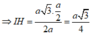
![]()
![]()
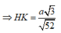
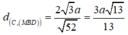
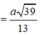
Đáp án B.

Gọi H là trung điểm AB, G là trọng tâm
Trong mặt phẳng (ABCD), ![]()
Ta có: ![]()
Gọi I là hình chiếu của H lên BD, K là hình chiếu của H lên GI
![]()
Ta có: 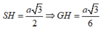
![]()
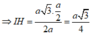
![]()
![]()
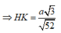
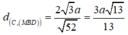
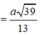
Cho hình chóp S.ABCD có đáy là hình chữ nhật, AB =a, AD = 2a. Tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy. Góc giữa đường thẳng SC và mặt phẳng (ABCD) bằng 45 0 .Gọi M là trung điểm của SD. Tính theo a khoảng cách d từ điểm M đến mặt phẳng (SAC)
A. d = a 1315 89
B. d = a 1513 89
C. d = 2 a 1315 89
D. d = 2 a 1513 89
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. Gọi I là trung điểm của AB và M là trung điểm của AD. Khoảng cách từ I đến mặt phẳng (SMC) bằng:
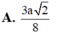
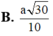

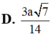
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = a, AD = 2 3 . Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng (ABCD). Gọi M, N, P lần lượt là trung điểm của các cạnh SA, CD, CB. Tính côsin góc tạo bởi mặt phẳng (MNP) và (SCD).
A. 2 435 145
B. 11 435 145
C. 2 870 145
D. 3 145 145
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D, đáy nhỏ của hình thang là CD, cạnh bên SC= a 15 Tam giác SAD là tam giác đều cạnh bằng 2a và nằm trong mặt phẳng vuông góc với đáy. Gọi H là trung điểm AD, khoảng cách từ B đến mặt phẳng (SHC) bằng 2 a 6 Tính thể tích V của khối chóp S.ABCD?
![]()
![]()
![]()
![]()
Cho hình chóp S. ABCD có đáy là hình vuông ABCD cạnh a mặt phẳng (SAB) vuông góc với mặt phẳng đáy. Tam giác SAB đều, M là trung điểm của SA . Tính khoảng cách từ M đến mặt phẳng (SCD)
A. a 21 14
B. a 21 7
C. a 3 14
D. a 3 7
Cho hình chóp S.ABCD với đáy ABCD là hình thang vuông tại A và D, đáy nhỏ của hình thang là CD, cạnh bên SC= a 15 Tam giác SAD là tam giác đều cạnh 2a và nằm trong mặt phẳng vuông góc với đáy. Gọi H là trung điểm của cạnh AD, khoảng cách từ B tới mặt phẳng (SHC) bằng 2 6 a Tính thể tích V của khối chóp S.ABCD?
![]()
![]()
![]()
![]()
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Đường thẳng SA vuông góc với mặt phẳng đáy, SA = a. Gọi M là trung điểm của CD. Khoảng cách từ M đến mặt phẳng (SAB) là:
A . a 2 2
B . a
C . a 2
D . 2 a
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB =a, AD = 2a Cạnh bên SA vuông góc với mặt phẳng đáy và cạnh bên SC tạo với đáy một góc 60 o Gọi M, N là trung điểm các cạnh bên SA và SB Khoảng cách từ điểm S đến mặt phẳng (DMN) bằng
A. 2 a 465 31
B. a 31 31
C. a 60 31
D. 2 a 5 31
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B với AB = BC = a, AD = 2a. Cạnh bên SA vuông góc với đáy và SC tạo với (SAD) góc 30 o . Gọi G là trọng tâm tam giác SAB. Tính khoảng cách từ G đến mặt phẳng (SCD).