Các câu hỏi tương tự
Cho hình chóp S.ABCD đáy ABCD là hình bình hành. M, N lần lượt là trung điểm của AB và SC. I là giao điểm của AN và (SBD). J là giao điểm của MN với (SBD). Khi đó tỉ số I B I J là
A. 4
B. 3
C. 2
D. 1
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi K là trung điểm SC. Mặt phẳng (P) qua AK cắt các cạnh SB, SD lần lượt tại M, N. Gọi V và V’ lần lượt là thể tích các khối chóp S.ABCD và S.AMKN. Tỉ số
V
V
có giá trị nhỏ nhất bằng A.
1
5
B.
3
8
C.
1
3
D.
1...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi K là trung điểm SC. Mặt phẳng (P) qua AK cắt các cạnh SB, SD lần lượt tại M, N. Gọi V và V’ lần lượt là thể tích các khối chóp S.ABCD và S.AMKN. Tỉ số V ' V có giá trị nhỏ nhất bằng
A. 1 5
B. 3 8
C. 1 3
D. 1 2
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của các cạnh AB. SC và P là điểm trên cạnh SD sao cho
S
P
S
D
3
4
. Mặt phẳng (MNP) cắt cạnh SB tại điểm Q. Tỉ số
S
Q
S
B
bằng
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của các cạnh AB. SC và P là điểm trên cạnh SD sao cho S P S D = 3 4 . Mặt phẳng (MNP) cắt cạnh SB tại điểm Q. Tỉ số S Q S B bằng
![]()
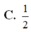
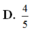
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M,N,P,Q,R lần lượt là trung điểm của AB,CD,SC,SB,BM. Mặt phẳng (SDM) không song song với đường thẳng nào dưới đây? A.Đường thẳng CQ. B.Đường thẳng BP. C. Đường thẳng NP. D. Đường thẳng QR.
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M,N,P,Q,R lần lượt là trung điểm của AB,CD,SC,SB,BM. Mặt phẳng (SDM) không song song với đường thẳng nào dưới đây?
A.Đường thẳng CQ.
B.Đường thẳng BP.
C. Đường thẳng NP.
D. Đường thẳng QR.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Hai mặt bên (SAB) và (SAD) cùng vuông góc với mặt đáy. Biết góc giữa hai mặt phẳng (SCD) và (ABCD) bằng
45
0
. Gọi lần lượt là thể tích khối chóp S.AHK và S.ACD với H; K lần lượt là trung điểm của SC và SD. Tính độ dài đường cao của khối chóp S.ABCD và tỉ số
k
V
1
V
2
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Hai mặt bên (SAB) và (SAD) cùng vuông góc với mặt đáy. Biết góc giữa hai mặt phẳng (SCD) và (ABCD) bằng 45 0 . Gọi lần lượt là thể tích khối chóp S.AHK và S.ACD với H; K lần lượt là trung điểm của SC và SD. Tính độ dài đường cao của khối chóp S.ABCD và tỉ số k = V 1 V 2
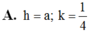
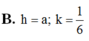
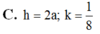
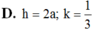
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là điểm trên cạnh SC sao cho 5SM2SC mặt phẳng
(
α
)
qua A, M và song song với đường thẳng BD cắt hai cạnh SB, SD lần lượt tại H, K. Tính tỉ số thể tích
V
S
.
A
H
M
K
V
S...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là điểm trên cạnh SC sao cho 5SM=2SC mặt phẳng ( α ) qua A, M và song song với đường thẳng BD cắt hai cạnh SB, SD lần lượt tại H, K. Tính tỉ số thể tích V S . A H M K V S . A B C D ?
A. 1 5
B. 8 35
C. 1 5
D. 6 35
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là điểm di động trên đoạn AB. Qua M vẽ mặt phẳng
α
song song với mặt phẳng (SBC), cắt các cạnh CD, DS, SA lần lượt tại các điểm N, P, Q. Tập hợp các giao điểm I của hai đường thẳng MQ và NP là A. Một đường thẳng. B. Nửa đường thẳng. C. Đoạn thẳng song song với AB. D. Tập hợp rỗng.
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là điểm di động trên đoạn AB. Qua M vẽ mặt phẳng α song song với mặt phẳng (SBC), cắt các cạnh CD, DS, SA lần lượt tại các điểm N, P, Q. Tập hợp các giao điểm I của hai đường thẳng MQ và NP là
A. Một đường thẳng.
B. Nửa đường thẳng.
C. Đoạn thẳng song song với AB.
D. Tập hợp rỗng.
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là điểm trên cạnh SC sao cho
5
S
M
2
S
C
, mặt phẳng
(
α
)
đi qua A, M và song song với đường thẳng BD cắt hai cạnh SB, SD lần lượt tại hai điểm H, K. Tính tỉ số thể tích
V
S
.
A
H
M
K...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là điểm trên cạnh SC sao cho 5 S M = 2 S C , mặt phẳng ( α ) đi qua A, M và song song với đường thẳng BD cắt hai cạnh SB, SD lần lượt tại hai điểm H, K. Tính tỉ số thể tích V S . A H M K V S . A B C D .
A. 1 5
B. 8 35
C. 1 5
D. 6 35
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi K là trung điểm SC. Mặt phẳng AK cắt các cạnh SB, SD lần lượt tại M và N. Gọi
V
1
, V theo thứ tự là thể tích khối tứ diện S.AMKN và hình chóp S.ABCD. Giá trị nhỏ nhất của tỷ số
V
1
V
bằng: A.
1
2
B.
2
3
C. ...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi K là trung điểm SC. Mặt phẳng AK cắt các cạnh SB, SD lần lượt tại M và N. Gọi V 1 , V theo thứ tự là thể tích khối tứ diện S.AMKN và hình chóp S.ABCD. Giá trị nhỏ nhất của tỷ số V 1 V bằng:
A. 1 2
B. 2 3
C. 1 3
D. 3 8