Các câu hỏi tương tự
Cho hình chóp S.ABCD có ABCD là hình vuông cạnh a, tam giác SAB đều và tam giác SCD vuông cân tại S. Tính diện tích mặt cầu ngoại tiếp hình chóp. A.
7
3
π
a
2
B.
8
3
π
a
2
C. ...
Đọc tiếp
Cho hình chóp S.ABCD có ABCD là hình vuông cạnh a, tam giác SAB đều và tam giác SCD vuông cân tại S. Tính diện tích mặt cầu ngoại tiếp hình chóp.
A. 7 3 π a 2
B. 8 3 π a 2
C. 5 3 π a 2
D. π a 2
Hình chóp tứ giác S.ABCD có đáy ABCD là hình vuông cạnh a. Tam giác SAB vuông cân tại S và tam giác SCD đều. Tính bán kính mặt cầu ngoài tiếp hình chóp S.ABCD.
Đọc tiếp
Hình chóp tứ giác S.ABCD có đáy ABCD là hình vuông cạnh a.
Tam giác SAB vuông cân tại S và tam giác SCD đều. Tính bán
kính mặt cầu ngoài tiếp hình chóp S.ABCD.
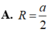
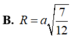
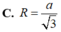
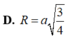
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a,
A
B
C
^
60
°
. Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính diện tích của mặt cầu ngoại tiếp hình chóp S.ABCD.
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, A B C ^ = 60 ° . Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính diện tích của mặt cầu ngoại tiếp hình chóp S.ABCD.
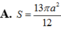
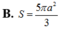
![]()
![]()
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, ADa,
A
B
3
a
,
∆
S
A
B
là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Tính theo a diện tích S của mặt cầu ngoại tiếp hình chóp S.ABCD.
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AD=a, A B = 3 a , ∆ S A B là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Tính theo a diện tích S của mặt cầu ngoại tiếp hình chóp S.ABCD.
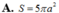
![]()
![]()
![]()
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a,
A
B
C
^
60
∘
.Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt đáy. Tính diện tích
S
m
c
của mặt cầu ngoại tiếp h...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, A B C ^ = 60 ∘ .Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt đáy. Tính diện tích S m c của mặt cầu ngoại tiếp hình chóp S.ABC.
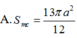
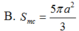
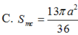
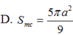
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a mặt bên SAB là tam giác đều, mặt bên SCD là tam giác vuông cân tại S, gọi M là điểm thuộc đường thẳng CD sao cho BM vuông góc với SA. Tính thể tích V của khối chóp S.BDM
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a mặt bên SAB là tam giác đều, mặt bên SCD là tam giác vuông cân tại S, gọi M là điểm thuộc đường thẳng CD sao cho BM vuông góc với SA. Tính thể tích V của khối chóp S.BDM
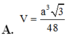
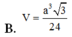
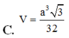
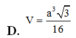
Cho hình chóp S.ABCD đáy ABCD là hình vuông cạnh 2a, tam giác SAB vuông cân tại S, tam giác SCD đều thì thể tích khối S.ABCD là: A.
4
a
3
3
3
B.
4
a
3
3
C.
2
a
3
3
D. ...
Đọc tiếp
Cho hình chóp S.ABCD đáy ABCD là hình vuông cạnh 2a, tam giác SAB vuông cân tại S, tam giác SCD đều thì thể tích khối S.ABCD là:
A. 4 a 3 3 3
B. 4 a 3 3
C. 2 a 3 3
D. 2 a 3 3 3
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, mặt bên SAB là tam giác cân tại S và nằm trong mặt phẳng vuông góc với (ABCD).Biết rằng côssin của góc giữa (SCD) và (ABCD) bằng
2
19
19
. Tính a theo thể tích V của khối chóp S.ABCD
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, mặt bên SAB là tam giác cân tại S và nằm trong mặt phẳng vuông góc với (ABCD).Biết rằng côssin của góc giữa (SCD) và (ABCD) bằng 2 19 19 . Tính a theo thể tích V của khối chóp S.ABCD
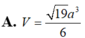
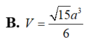
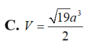
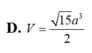
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, mặt bên SAB là tam giác cân tại S và nằm trong mặt phẳng vuông góc với (ABCD). Biết rằng côsin của góc giữa (SCD) và (ABCD) bằng
2
19
19
. Tính theo a thể tích V của khối chóp S.ABCD. A.
V
19
a
3
6
B.
V...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, mặt bên SAB là tam giác cân tại S và nằm trong mặt phẳng vuông góc với (ABCD). Biết rằng côsin của góc giữa (SCD) và (ABCD) bằng 2 19 19 . Tính theo a thể tích V của khối chóp S.ABCD.
A. V = 19 a 3 6
B. V = 15 a 3 6
C. V = 19 a 3 2
D. V = 15 a 3 6





