Đáp án là D
Ta có 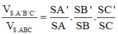
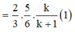
Theo giả thiết 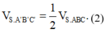
Từ (1) và (2) suy ra ![]()
Đáp án là D

Ta có 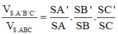
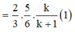
Theo giả thiết 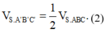
Từ (1) và (2) suy ra ![]()
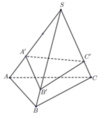
Cho khối chóp S.ABC, trên ba cạnh SA, SB, SC lần lượt lấy ba điểm A', B', C' sao cho SA' = 1 2 SA; SB' = 1 3 SB; SC' = 1 4 SC. Gọi V và V' lần lượt là thể tích của khối chóp S.ABC và S.A'B'C'. Khi đó tỉ số V ' V là:
A. 12
B. 1 12
C. 24
D 1 24
Cho hình chóp S.ABC với SA⊥SB, SB⊥SC, SC⊥SA, SA=SB=SC=a. Gọi B′,C′ lần lượt là hình chiếu vuông góc của S trên AB,AC. Thể tích của hình chóp S.AB′C′ là
![]()
![]()
![]()
![]()
Cho hình chóp S.ABC biết rằng SA, SB, SC vuông góc với nhau từng đôi một. Trên cạnh SA, SB, SC lần lượt lấy 3 điểm A', B', C' sao cho \(\Delta A'B'C'\) và \(\Delta ABC\) là hai tam giác đồng dạng. Hỏi có thể suy ra được mp(A'B'C') // mp(ABC) hay không?
Cho khối chóp S.ABC có SA = SB = SC = a và A S B ^ = B S C ^ = C S A ^ = 30 0 . Mặt phẳng ( α ) qua A và cắt hai cạnh SB, SC tại B', C' sao cho chu vi tam giác AB'C' nhỏ nhất. Tính k = V S . A B ' C ' V S . A B C .
![]()
![]()
![]()
![]()
Cho khối chóp S.ABC có các điểm A', B', C' lần lượt thuộc các cạnh SA, SB, SC thỏa 3SA' = SA, 4SB' = SB, 5SC' = 3SC. Biết thể tích khối chóp S.A'B'C' bằng 5 ( c m 3 ). Tìm thể tích khối chóp S.ABC
A. 120 ( c m 3 )
B. 60 ( c m 3 )
C. 80 ( c m 3 )
D. 100 ( c m 3 )
Cho hình chóp S.ABC, trên cạnh SB, SC, SD lần lượt lấy ba điểm A’, B’, C’sao cho SA = 2SA’; SB = 3SB’và SC = 4SC’. Gọi V lần lượt là thể tích của khối chóp S.A’B’C’và S.ABC. Khi đó tỉ số V ' V bằng bao nhiêu?
A. 12
B. 24.
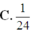
![]()
Cho hình chóp S.ABCD có đáy là hình thoi ABCD và có cạnh SA vuông góc với mặt phẳng (ABCD). Gọi I và K là hai điểm lần lượt lấy trên hai cạnh SB và SD sao cho SI/SB = SK/SD . Chứng minh:
a) BD ⊥ SC
b) IK ⊥mp(SAC)
Cho hình chóp S.ABCD có SA vuông góc với đáy. Mặt phẳng (a) qua A vuông góc với SC tại H. cắt SB, SD lần lượt tại 1 và K. Mặt phẳng qua I, K song song với SC cắt các cạnh BC,CD lần lượt tại E và F. Biết SC hợp với đáy một góc 60°. Tính diện tích tứ giác AECF, biết diện tích tứ giác AIHK bằng 10.
A. 12√3.
B. 20√3 3
C. 8√3 3
D. 4√3.
cho hình chóp S.ABCD có đáy hình vuông cạnh a, SA = a, SA ⊥ (ABCD). Gọi H, K lần lượt là trung điểm của cạnh SB,SD; O là tâm hình vuông ABCD.
1/ Chứng minh: (SAB) ⊥ (SBC)
2/ Chứng minh: SC ⊥ (AHK)