Chọn đáp án A
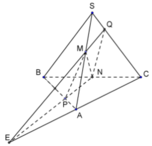
Trong mặt phẳng (ABC), gọi E = NP ∩ AC
Khi đó Q chính là giao điểm của SC với EM
Áp dụng định lý Menelaus vào tam giác ABC ta có:
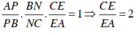
Áp dụng định lý Menelaus vào tam giác SAC ta có:
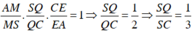
Chọn đáp án A

Trong mặt phẳng (ABC), gọi E = NP ∩ AC
Khi đó Q chính là giao điểm của SC với EM
Áp dụng định lý Menelaus vào tam giác ABC ta có:
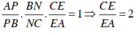
Áp dụng định lý Menelaus vào tam giác SAC ta có:
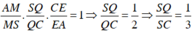
Câu 5: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P lần lượt là trung điểm của các cạnh SB, SD và BC. Gọi E là giao điểm của mặt phẳng (MNP) với cạnh SA. Tính tỉ số SE SA . A. 1 4 . B. 1 2 . C. 1 3 . D. 3
Cho hình chóp S.ABCD có đáy ABCD là hình vuông. Gọi M, N, P lần lượt là trung điểm của AB, BC và SC. a. Tìm giao tuyến của các mặt phẳng: (SAD) và (SBC). b. Tìm giao điểm I của BC với mặt phẳng (MNP).
Cho hình chóp S. ABCD. Lấy M, N và P lần lượt là các điểm trên các đoạn SA, AB và BC sao cho chúng không trùng với trung điểm của các đoạn thẳng ấy. Tìm giao điểm ( nếu có) của mặt phẳng (MNP) với các cạnh của hình chóp.
Cho hình chóp S.ABCD. Gọi M, N lần lượt là trung điểm của cạnh SA, SD, P là điểm thuộc cạnh SB sao cho: SP = 3 PB. Gọi O là giao điểm của AC và BD; E là giao điểm của PN và SO. Tìm giao điểm Q của SC và (MNP).
A. Q là giao điểm của ME và SA
B. Q là giao điểm của MO và SC
C. Q là giao điểm của SC và PE
D. Q là giao điểm của ME và SC
Cho hình chóp S.ABCD có đáy ABCD là hình vuông. Gọi M, N, P lần lượt là trung điểm của AB, BC và SC. a. Tìm giao tuyến của các mặt phẳng: (SAB) và (SCD) b. Tìm giao điểm I của AD với mặt phẳng (MNP)
cho hình chóp SABCD đáy ABCD là hình chữ nhật AB= a ,AD=2a,SA=SB=SC=SD=2a gọi O là giao điểm của AC và BD
a chứng minh mặt phẳng SAC vuông góc với mặt phẳng ABCD
b tính khoảng cách từ O->mặt phẳng SCD
c gọi M,N lần lượt là trung điểm của các cạnh SA và BC tính sin góc MN,CSBD
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với mặt đáy. Gọi M là trung điểm của BC. Mặt phẳng (P) đi qua A và vuông góc với SM cắt SB, SC lần lượt tại E, F. Biết 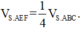 Tính thể tích V của khối chóp S.ABC
Tính thể tích V của khối chóp S.ABC
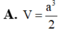
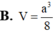
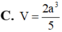
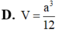
Cho hình chóp S. ABCD. Lấy M, N và P lần lượt là các điểm trên các đoạn SA, AB và BC sao cho chúng không trùng với trung điểm của các đoạn thẳng ấy. Tìm giao tuyến ( nếu có) của mặt phẳng (MNP) với các mặt của hình chóp.
Câu 4: (0.5 điểm) ) Cho hình chóp S.ABC , gọi M, N lần lượt là trung điểm của các cạnh SA, SC. Biết G là trọng tâm của tam giác ABC. Tìm giao điểm của đường thẳng SG và mặt phẳng (BMN)