Đáp án C
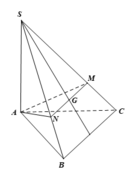
Qua G kẻ MN//BC(M ∈ SC, N ∈ SB)

![]()
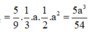
Đáp án C

Qua G kẻ MN//BC(M ∈ SC, N ∈ SB)

![]()
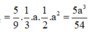
hình chóp S.ABC có SA vuông góc với mp(ABC) và đáy ABC là tam giác vuông cân tại C, AB = a. Gọi H là hình chiếu vuông góc của A lên đường thẳng SC, khoảng cách từ C đến mp(AHB) bằng \(\frac{a}{3}\) . Thể tích khối chóp S.ABC là?
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O cạnh bằng a, A B C ^ = 60 0 , SA=SB=SC, SD= 2a. Gọi (P) là mặt phẳng qua A và vuông góc với SB tại K. Mặt phẳng (P) chia khối chóp S.ABCD thành hai phần có thể tích V 1 ; V 2 trong đó V 1 là thể tích khối đa diện chứa đỉnh S. Tính V 1 V 2
A. 11
B. 7
C. 9
D. 4
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại C ; SA vuông góc với đáy; SC = a. Gọi α là góc giữa hai mặt phẳng (SBC) và (ABC). Tính để thể tích khối chóp S.ABC lớn nhất
![]()
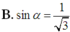
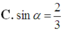
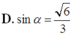
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với mặt đáy. Gọi M là trung điểm của BC. Mặt phẳng (P) đi qua A và vuông góc với SM cắt SB, SC lần lượt tại E, F. Biết 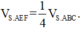 Tính thể tích V của khối chóp S.ABC
Tính thể tích V của khối chóp S.ABC
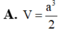
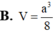
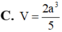
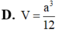
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, AB =a. Đường thẳng vuông góc với mặt phẳng ( ABC) và S A = a 3 Tính thể tích V của khối chóp S.ABC
A. 2 a 3 6
B. 3 a 3 6
C. 2 a 3 2
D. 3 a 3 2
Cho hình chóp S. ABCD có đáy ABCD là hình bình hành có thể tích là V. Gọi M là một điểm trên cạnh AB sao cho M A A B = x , 0< x < 1. . Biết rằng mặt phẳng α qua M và song song với (SBC) chia khối chóp S. ABCD thành hai phần trong đó phần chứa điểm A thể tích bằng 4 27 V . Tính giá trị của biểu thức 1 - x 1 + x
A. 1 2
B. 1 5
C. 1 3
D. 3 5
Cho hình chóp S.ABCD, có đáy là hình vuông cạnh a và tam giác ABC đều. Một điểm M thuộc cạnh BC sao cho BM= x ( 0< x< a), mặt phẳng (α) đi qua M song song với SA và SB. Biết rằng mp (α) cắt hình chóp theo 1 tứ giác. Tính diện tích thiết diện theo a và x
A. 3 4 a 2 - x 2
B. 3 2 a 2 - x 2
C. 2 4 a 2 - x 2
D. 1 4 a 2 - x 2
Cho hình chóp S.ABC có SC= 2a, S C ⊥ ( A B C ) Đáy ABC là tam giác vuông cân tại B và có ( α ) Mặt phẳng ( α ) đi qua C và vuông góc với SA, cắt SA, SB lẩn lượt tại D, E. Tính thể tích khối chóp S.CDE.
A. 4 a 3 9
B. 2 a 3 3
C. 2 a 3 9
D. a 3 3
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B và cạnh bên SA vuông góc với mặt phẳng (ABC). Biết rằng AB = a, AC = a 3 và S B A ^ = 60 0 . Gọi H là hình chiếu vuông góc của A trên cạnh SC. Tính tỷ số thể tích của hai khối SABH và HABC.
A . 3 4
B . 1 12
C . 3 2
D . 7 4