Đúng/ sai

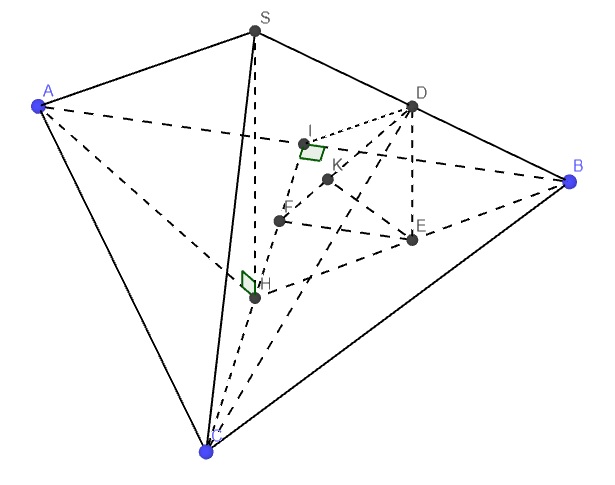
Cho hình chóp \( S.ABC \) có đáy là tam giác đều cạnh bằng \( \sqrt{3} \). Gọi \( I \) là trung điểm của \( AB \), hình chiếu vuông góc của \( S \) lên mặt phẳng \( (ABC) \) là trung điểm \( H \) của \( CI \). Biết góc giữa \( SA \) và mặt phẳng \( (ABC) \) bằng \( 45^\circ \). Giả sử \( G \) là trọng tâm tam giác \( SBC \). Xét tính đúng sai của các mệnh đề sau:
a) \( SH = \frac{\sqrt{21}}{4} \).
b) Thể tích khối chóp \( S.ABC \) bằng \( \frac{3\sqrt{7}}{16} \).
c) Góc giữa \( SA \) và mặt phẳng \( (ABC) \) là góc \( SAC \).
d) Khoảng cách giữa hai đường thẳng \( SA \) và \( CG \) bằng \( \frac{\sqrt{231}}{22} \).
Vấn đề bạn cần hỏi chắc chỉ nằm ở câu d
Ko cần quan tâm điểm G, gọi D là trung điểm của SB thì \(G\in CD\) nên \(d\left(SA;CG\right)=d\left(SA;CD\right)\)
Mặt khác \(DI||SA\) (đường trung bình) nên
\(SA||\left(CDI\right)\Rightarrow d\left(SA;CD\right)=d\left(A;\left(CDI\right)\right)=d\left(B;\left(CDI\right)\right)\) do I là trung điểm AB
Gọi E là trung điểm BH \(\Rightarrow DE||SH\) (đường trung bình) \(\Rightarrow DE\perp\left(ABC\right)\)
Từ E kẻ EF vuông góc CI, kẻ EK vuông góc DF \(\Rightarrow DK=d\left(E;\left(CDI\right)\right)=\dfrac{1}{2}d\left(B;\left(CDI\right)\right)\)
\(EF=\dfrac{1}{2}BI=\dfrac{1}{4}AB=\dfrac{\sqrt{3}}{4}\) (đường trung bình)
\(DE=\dfrac{1}{2}SH=\dfrac{\sqrt{21}}{8}\)
\(\Rightarrow d\left(SA;CG\right)=2DK=2.\dfrac{EF.DE}{\sqrt{EF^2+DE^2}}=\dfrac{\sqrt{399}}{38}\) (có tính sai ko nhỉ)