Question

cho hình chóp SABC có đáy là tam giác ABC vuông cân tại B, AC=a\(\sqrt{2}\)  và SA vuông góc với đáy, góc giữa (SBC) và (ABC)=30. Gọi H và K lần lượt là trung điểm AC và SB.c/m thể tích khối chóp S.HKC bằng 1/4 thể tích khối chóp S.ABC

Answer 1

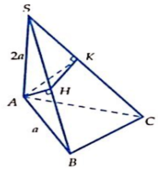
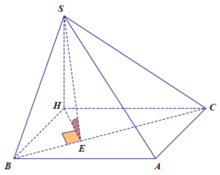
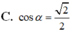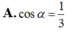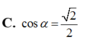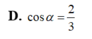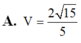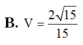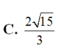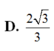Câu này có thể chứng minh mà ko cần tính ra thể tích cụ thể:

\(HC=\dfrac{1}{2}AC\Rightarrow S_{\Delta SHC}=\dfrac{1}{2}S_{\Delta SAC}\) \(\Rightarrow\dfrac{S_{\Delta SHC}}{S_{\Delta SAC}}=\dfrac{1}{2}\)

\(\left\{{}\begin{matrix}BK\cap\left(SAC\right)=S\\BS=2KS\end{matrix}\right.\) \(\Rightarrow d\left(B;\left(SAC\right)\right)=2d\left(K;\left(SAC\right)\right)\)

\(\Rightarrow\dfrac{d\left(K;\left(SAC\right)\right)}{d\left(B;\left(SAC\right)\right)}=\dfrac{1}{2}\)

\(\Rightarrow\dfrac{V_{S.HKC}}{V_{S.ABC}}=\dfrac{\dfrac{1}{3}.d\left(K;\left(SAC\right)\right).S_{\Delta SHC}}{\dfrac{1}{3}d\left(B;\left(SAC\right)\right).S_{\Delta SAC}}=\dfrac{d\left(K;\left(SAC\right)\right)}{d\left(B;\left(SAC\right)\right)}.\dfrac{S_{\Delta SHC}}{S_{\Delta SAC}}=\dfrac{1}{2}.\dfrac{1}{2}=\dfrac{1}{4}\)