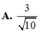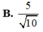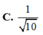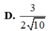Các câu hỏi tương tự
Đặt câu hỏi Cho hình chóp SABC, có đáy ABC là tam giác vuông cân với BA = BC = a; SA (ABC) và SA = a. Gọi E, F lần lượt là trung điểm của các cạnh AB và AC. a) Tính góc giữa hai mặt phẳng (SAC) và (SBC). b) Tính góc giữa 2 mặt phẳng (SEF) và (SBC). Giúp với ạ
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, BC a, cạnh bên SA vuông góc với đáy, SA a
3
. Gọi M là trung điểm của AC. Tính cotang góc giữa hai mặt phẳng (SBM) và (SAB). A.
3
2
B. 1 C.
21
7
D.
2
7
7
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, BC = a, cạnh bên SA vuông góc với đáy, SA = a 3 . Gọi M là trung điểm của AC. Tính cotang góc giữa hai mặt phẳng (SBM) và (SAB).
A. 3 2
B. 1
C. 21 7
D. 2 7 7
Cho hình chóp S.ABC có đáy là tam giác ABC vuông cân ở B,
A
C
a
2
. SA vuông góc với mặt phẳng (ABC) và SAa. Gọi G là trọng tâm của tam giác SBC. Một mặt phẳng đi qua hai điểm A, G và song song với BC cắt SB, SC lần lượt tại B và C. Thể tích khối chóp S.ABC bằng:
Đọc tiếp
Cho hình chóp S.ABC có đáy là tam giác ABC vuông cân ở B, A C = a 2 . SA vuông góc với mặt phẳng (ABC) và SA=a. Gọi G là trọng tâm của tam giác SBC. Một mặt phẳng đi qua hai điểm A, G và song song với BC cắt SB, SC lần lượt tại B' và C'. Thể tích khối chóp S.A'B'C' bằng:
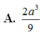
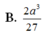
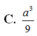
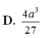
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B,BCa, cạnh bên SA vuông góc với đáy ,SAasqrt[]{3} .Gọi M là trung điểm của AC.Tính cot góc giữa hai mặt phẳng left(SBMright) và left(SABright).
Đọc tiếp
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông cân tại \(B\),\(BC=a\), cạnh bên \(SA\) vuông góc với đáy ,\(SA=a\sqrt[]{3}\) .Gọi \(M\) là trung điểm của \(AC\).Tính cot góc giữa hai mặt phẳng \(\left(SBM\right)\) và \(\left(SAB\right)\).
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, mặt bên SBC là tam giác đều cạnh a và mặt phẳng (SBC) vuông góc với mặt đáy. Tính theo a khoảng cách giữa hai đường thẳng SA và BC.
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, mặt bên SBC là tam giác đều cạnh a và mặt phẳng (SBC) vuông góc với mặt đáy. Tính theo a khoảng cách giữa hai đường thẳng SA và BC.
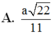
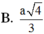
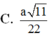
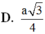
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, mặt bên SBC là tam giác đều cạnh a và mặt phẳng (SBC) vuông góc với mặt đáy. Tính theo a khoảng cách giữa hai đường thẳng SA và BC. A.
a
22
11
B.
a
4
3
C.
a...
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, mặt bên SBC là tam giác đều cạnh a và mặt phẳng (SBC) vuông góc với mặt đáy. Tính theo a khoảng cách giữa hai đường thẳng SA và BC.
A. a 22 11
B. a 4 3
C. a 11 22
D. a 3 4
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, BC = 2a, SA = a và SA vuông góc (ABC). Tính góc giữa hai mặt phẳng (SBC) và (ABC)
A. 45 °
B. 30 °
C. 60 °
D. 90 °
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, mặt bên SBC là tam giác đều cạnh a và mặt phẳng (SBC) vuông góc với mặt đáy. Khoảng cách giữa hai đường thẳng SA và BC là A.
2
a
2
B.
a
2
C.
3
a
4
D.
3
a...
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, mặt bên SBC là tam giác đều cạnh a và mặt phẳng (SBC) vuông góc với mặt đáy. Khoảng cách giữa hai đường thẳng SA và BC là
A. 2 a 2
B. a 2
C. 3 a 4
D. 3 a 2
Cho hình chóp S.ABC có đáy là tam giác vuông cân cạnh bằng B, cạnh bên SA vuông góc với mặt phẳng đáy, ABBCa và SAa. Góc giữa hai mặt phẳng (SAC) và (SBC) bằng
Đọc tiếp
Cho hình chóp S.ABC có đáy là tam giác vuông cân cạnh bằng B, cạnh bên SA vuông góc với mặt phẳng đáy, AB=BC=a và SA=a. Góc giữa hai mặt phẳng (SAC) và (SBC) bằng
![]()
![]()
![]()
![]()