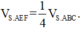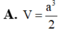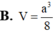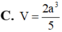Gọi D là hình chiếu vuông góc của S lên (ABC)
\(SD\perp\left(ABC\right)\Rightarrow SD\perp AB\) , mà \(AB\perp SA\left(gt\right)\Rightarrow AB\perp\left(SAD\right)\Rightarrow AB\perp AD\)
\(\Rightarrow AD||BC\)
Tương tự ta có: \(BC\perp\left(SCD\right)\Rightarrow BC\perp CD\Rightarrow CD||AB\)
\(\Rightarrow\) Tứ giác ABCD là hình vuông
\(\Rightarrow BD=a\sqrt{2}\)
\(SD=\sqrt{SB^2-BD^2}=a\sqrt{2}\)
Gọi P là trung điểm AD \(\Rightarrow MP\) là đường trung bình tam giác SAD
\(\Rightarrow\left\{{}\begin{matrix}MP=\dfrac{1}{2}SD=\dfrac{a\sqrt{2}}{2}\\MP||SD\Rightarrow MP\perp\left(ABC\right)\end{matrix}\right.\)
\(\Rightarrow\alpha=\widehat{MNP}\)
\(cos\alpha=\dfrac{NP}{MN}=\dfrac{NP}{\sqrt{NP^2+MP^2}}=\dfrac{a}{\sqrt{a^2+\dfrac{a^2}{2}}}=\dfrac{\sqrt{6}}{3}\)