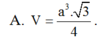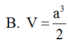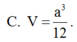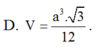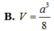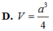Phương pháp:
+ Sử dụng định nghĩa để tìm góc giữa hai mặt phẳng (P) và (Q):
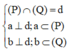khi đó góc giữa (P) và (Q) chính là góc giữa hai đường thẳng a và b.
+ Diện tích tam giác đều cạnh a được tính theo công thức S = a 2 3 4
+ Tính thể tích V = 1 3 S.h với S là diện tích đáy, h là chiều cao hình chóp.
Cách giải:
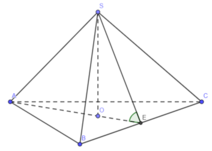
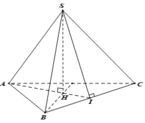
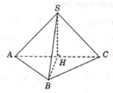
Gọi E là trung điểm của BC, O là trọng tâm tam giác ABC => SO ⊥ (ABCD) (do S.ABC là hình chóp đều)
Suy ra AE ⊥ BC (do ∆ ABC đều) và SE ⊥ BC (do ∆ SBC cân tại S)
Ta có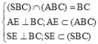 
nên góc giữa (ABC) và (SBC) là SEA.
Từ giả thiết suy ra SEA = 60 ° .
Tam giác ABC đều cạnh a 
Xét tam giác SOE vuông tại O (do SO ⊥ (ABC)=> SO ⊥ AE), ta có:
Diện tích tam giác đều ABC là: 
Vậy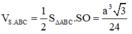 
Chọn A
