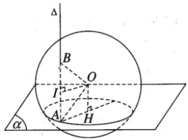
Gọi H là hình chiếu vuông góc của tâm O trên mặt phẳng ( α ). Theo giả thiết ta có ∠ OAH = 30 °
Do đó:

Vậy diện tích của thiết diện tạo bởi ( α ) và hình cầu là:
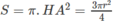

Gọi H là hình chiếu vuông góc của tâm O trên mặt phẳng ( α ). Theo giả thiết ta có ∠ OAH = 30 °
Do đó:

Vậy diện tích của thiết diện tạo bởi ( α ) và hình cầu là:
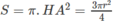
Cho hình cầu tâm O bán kính r. Lấy một điểm A trên mặt cầu và gọi ( α ) là mặt phẳng đi qua A sao cho góc giữa OA và ( α ) bằng 30 ° . Đường thẳng đi qua A vuông góc với mặt phẳng ( α ) cắt mặt cầu tại B. Tính độ dài đoạn AB.
Cho mặt cầu tâm O bán kính r. Gọi ( α ) là mặt phẳng cách tâm O một khoảng h (0 < h < r) và cắt mặt cầu theo đường tròn (C). Đường thẳng d đi qua một điểm A cố định trên (C) và vuông góc với mặt phẳng ( α ) cắt mặt cầu tại một điểm B. Gọi CD là đường kính di động của (C). Với vị trí nào của CD thì diện tích tam giác BCD lớn nhất?
Cho hai đường thẳng chéo nhau ∆ và ∆ ′ có AA’ là đoạn vuông góc chung, trong đó A ∈ ∆ và A′ ∈ ∆ ′. Gọi ( α ) là mặt phẳng chứa AA’ và vuông góc với ∆ ′ và cho biết AA’ = a. Một đường thẳng thay đổi luôn luôn song song với mặt phẳng ( α ) lần lượt cắt ∆ và ∆ ′ tại M và M’ . Hình chiếu vuông góc của M trên mặt phẳng ( α ) là M 1 . Xác định tâm O và bán kính r của mặt cầu đi qua 5 điểm A, A’ , M , M’, M 1 . Tính diện tích của mặt cầu tâm O nói trên theo a, x = A’M’ và góc φ = ( ∆ , ∆ ′)
Cho mặt cầu tâm O bán kính r. Gọi ( α ) là mặt phẳng cách tâm O một khoảng h (0 < h < r) và cắt mặt cầu theo đường tròn (C). Đường thẳng d đi qua một điểm A cố định trên (C) và vuông góc với mặt phẳng ( α ) cắt mặt cầu tại một điểm B. Gọi CD là đường kính di động của (C). Tìm tập hợp các điểm H, hình chiếu của B trên CD khi CD chuyển động trên đường tròn (C).
Cho mặt cầu tâm O bán kính r. Gọi ( α ) là mặt phẳng cách tâm O một khoảng h (0 < h < r) và cắt mặt cầu theo đường tròn (C). Đường thẳng d đi qua một điểm A cố định trên (C) và vuông góc với mặt phẳng ( α ) cắt mặt cầu tại một điểm B. Gọi CD là đường kính di động của (C). Chứng minh các tổng AD 2 + BC 2 và AC 2 + BD 2 có giá trị không đổi
Một hình trụ có các đáy là hai hình tròn tâm O và O’ bán kính r và có đường cao h = r 2 . Gọi A là một điểm trên đường tròn tâm O và B là một điểm trên đường tròn tâm O’ sao cho OA vuông góc với O’B. Gọi ( α ) là mặt phẳng qua AB và song song với OO’. Tính khoảng cách giữa trục OO’ và mặt phẳng (α).
Trong mặt phẳng ( α ) cho hình vuông ABCD có cạnh bằng a. Trên đường thẳng Ax vuông góc với ( α ) ta lấy một điểm S tùy ý, dựng mặt phẳng ( β ) đi qua A và vuông góc với đường thẳng SC. Mặt phẳng ( β ) cắt SB, SC, SD lần lượt tại B’ , C’, D’. Tính diện tích của mặt cầu đó và tính thể tích khối cầu được tạo thành.
Cho hình cầu đường kính AA’ = 2r. Gọi H là một điểm trên đoạn AA’ sao cho AH = 4r/3. Mặt phẳng ( α ) qua H và vuông góc với AA’ cắt hình cầu theo đường tròn (C). Tính diện tích của hình tròn (C) .
Cho hình vuông ABCD cạnh a. Từ tâm O của hình vuông dựng đường thẳng Δ vuông góc với mặt phẳng (ABCD). Trên Δ lấy điểm S sao cho OS = a/2 . Xác định tâm và bán kính mặt cầu ngoại tiếp hình chóp S.ABCD. Tính diện tích mặt cầu và thể tích khối cầu được tạo nên bởi mặt cầu đó.