Các câu hỏi tương tự
Cho hình bình hành ABCD. O là giao điểm của 2 đg chéo. Trên cac cạnh AB, BC, CD,DA ta lần lượt lấy các điểm E,F,G,H sao cho AE=CG,BF=DH
a, Xác định tâm đối xứng cưa hình bình hành ABCD
b, CM : EFGH là hình bình hành, tìm tâm đối xứng của nó
c, O còn là tâm đối xứng của hình bình hành nào?
Cho hình bình hành ABCD. O là giao điểm của 2 đg chéo.Trên các cạnh AB, BC, CD,DA ta lần lượt lấy các điểm E,F,G,H sao cho AE=CG, BF=DH
a, Xác định tâm đối xứng của hình bình hành ABCD
b, Chứng minh EFGH là hình bình hành, tìm tâm đối xứng của nó
c, O còn là tâm đối xứng của những hình bình hành nào ?
Cho hình bình hành ABCD. O là giao điểm của hai đường chéo. Trên các cạnh AB, BC, CD, DA ta lần lượt lấy các điểm E, F, G, H sao cho AE = CG, BF = DH. Chứng minh EFGH là hình bình hành, tìm tâm đối xứng của nó.
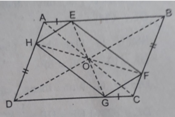
Cho hình bình hành ABCD. O là giao điểm của hai đường chéo. Trên các cạnh AB, BC, CD, DA ta lần lượt lấy các điểm E, F, G, H sao cho AE = CG, BF = DH. Xác định tâm đối xứng của hình bình hành ABCD.
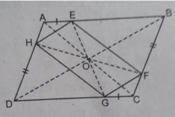
Cho hình bình hành ABCD. O là giao điểm của hai đường chéo. Trên các cạnh AB, BC, CD, DA ta lần lượt lấy các điểm E, F, G, H sao cho AE = CG, BF = DH. O còn là tâm đối xứng của những hình bình hành nào?
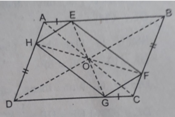
Bài 4 (3,0 điểm). Cho hình bình hành ABCD. Trên cạnh AB lấy điểm E, trên cạnh CD lấy điểm F sao cho AE = CF. a) Chứng minh tứ giác AECF là hình bình hành. b) Chứng minh DE = BF c) Gọi O là giao điểm của AC và BD. I là điểm đối xứng của A qua D. Chứng minh OD // CI. d) Chứng minh BD, EF, AC đồng quy tại một điểm.
Cho hình thoi ABCD tâm O. Trên tia đối của các tia BA, CB, DC, AD lần lượt các điểm E, F, G, H sao cho BE = CF = DG = AH.
a) Chứng minh tứ giác EFGH là hình bình hành.
b) Chứng minh điểm O là tâm đối xứng của hình bình hành EFGH.
c) Hình thoi ABCD phải có điều kiện gì để EFGH trở thành hình thoi ?
cho hình bình hành ABCD trên AB và CD lấy các điểm E,F sao cho AE=CF gọi O là giao điểm của AC và BD. CMR: E,F đối xứng nhau qua O
Cho hình bình hành ABCD, trên cạnh AB lấy điểm E và trên cạnh CD lấy điểm F sao cho AE = CF. Gọi O là giao điểm của AC và BD. Chứng minh E và F đối xứng qua O.






