a) Trong đường tròn nhỏ:
AB > CD => OH < OK (định lí 3)
b) Trong đường tròn lớn:
OH < OK => ME > MF (định lí 3)
c) Trong đường tròn lớn:
ME > MF => MH > MK
a) Trong đường tròn nhỏ:
AB > CD => OH < OK (định lí 3)
b) Trong đường tròn lớn:
OH < OK => ME > MF (định lí 3)
c) Trong đường tròn lớn:
ME > MF => MH > MK
Cho hình 70 trong đó hai đường tròn cùng có tâm là O. Cho biết AB > CD.
Hãy so sánh các độ dài:
OH và OK
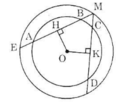
Hình 70
Cho hình 70 trong đó hai đường tròn cùng có tâm là O. Cho biết AB > CD.
Hãy so sánh các độ dài:
ME và MF
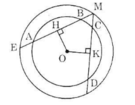
Hình 70
Cho hình 70 trong đó hai đường tròn cùng có tâm là O. Cho biết AB > CD.
MH và MK
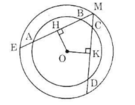
Hình 70
Cho nửa đường tròn tâm O , đường kính AB. Từ A và B kẻ các tiếp tuyến à và By, Qua M thuộc nửa đường tròn, kẻ tiếp tuyến thứ 3 cắt Ax và By lần lượt tại E và F.
a) CMR: 4 điểm A,E,M,O cùng thuộc 1 đường tròn.
b) AM cắt OE tại P. BM cắt OF tại Q.Tứ giác MPOQ là hình j? Vì sao?
c) Kẻ MH vuông AB tại H.Gọi K là giao điểm của MH và BE. So sánh MK và KH
Cho hai đường tròn đồng tâm O. Gọi AB là dây bất kì của đường tròn nhỏ. Đường thẳng AB cắt đường tròn lớn ở C và D (A nằm giữa B và C). So sánh các độ dài AC và BD.
Bài 1: Cho đường tròn (O), đường kính AB, dây CD vuông góc với AB tại điểm H thuộc bán kính OA. Gọi M là điểm thuộc bán kính OB, E và F theo thứ tự là giao điểm của CM và DM với đường tròn (E khác C, F khác D). Chứng minh rằng: a) MC = MD b) ME = MF
Bài 2: Cho đường tròn (O) đường kính AB. Vẽ các dây BC, BD thuộc hai nửa mặt phẳng đối nhau bờ AB sao cho BD > BC. So sánh độ dài hai dây AD và AC.
Bài 3. Cho đường tròn (O), hai dây AB và AC vuông góc với nhau có độ dài theo thứ tự bằng 10cm và 24cm. a) Tính khoảng cách từ tâm đến mỗi dây b) chứng minh rằng ba điểm B, O, C thẳng hàng.
Bài 4. Cho đường tròn (O), hai dây AB và CD bằng nhau, các tia AB và CD cắt nhau tại điểm M nằm ngoài đường tròn. Trên tia đối của tia AB lấy điểm E sao cho AE = BM. Trên tia đối của tia CD lấy điểm F sao cho CF = DM. Chứng minh rằng OE = OF.
Bài 5. Cho đường tròn (O), hai dây AB và CD có AB > CD, các tia AB và CD cắt nhau tại điểm M nằm ngoài đường tròn. Gọi H và K theo thứ tự là trung điểm của AB và CD. So sánh các độ dài MH và MK.
giải giúp mình vs ạ . tạo mình đang cần gấp . cảm ơn nha
Bài 1: Cho AB và CD là 2 dây của đường tròn O cắt nhau tại M nằm bên trong đường tròn gọi H, K lần lượt là trung điểm của AB, CD biết AB> CD. So sánh MH và MK
Bài 2: Cho đường tròn tâm O bán kính AB vẽ 2 dây AB và CD // với nhau. CMR:
a) AC = BD
b) 3 điểm C, O, D thẳng hàng
( Chú ý: BONUS THÊM HÌNH CÀNG TỐT )
Cho nửa đường tròn (O) đường kính AB. Lấy M là điểm tuỳ ý trên nửa đường tròn (M khác A và B). Kẻ MH vuông góc với AB (H ∈ AB). Trên cùng nửa mặt phang bờ AB chứa nửa đường tròn (O) vẽ hai nửa đường tròn tâm O 1 , đường kính AH và tâm O 2 , đường kính BH. Đoạn MA và MB cắt hai nửa đường tròn ( O 1 ) và ( O 2 ) lần lượt tại P và Q. Chứng minh:
a, MH = PQ
b, Các tam giác MPQ và MBA đồng dạng
c, PQ là tiếp tuyến chung của hai đường tròn ( O 1 ) và ( O 2 )
Cho đường tròn tâm O, đường kính AB, vẽ hai dây AB CD song song nhau. kẽ OI vuông góc AC a) Chứng minh OI vuông góc BD tại K. b ) Chứng minh tam giác IOA = tam giác OKB. c) So sánh AC và BD