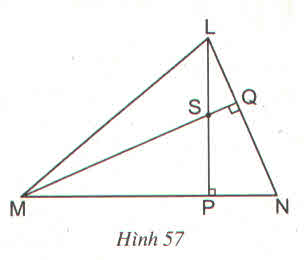
a) Từ hình vẽ ta có: LP ⊥ MN; MQ ⊥ LN
ΔMNL có S là giao điểm của hai đường cao LP và MQ nên S chính là trực tâm của tam giác (định lí ba đường cao).
=> NS cũng là đường cao trong tam giác hay NS ⊥ LM (đpcm).
b) ΔNMQ vuông tại Q có góc LNP = 50o nên góc QMN = 40o
ΔMPS vuông tại P có góc QMP = 40o nên góc MSP = 50o
Vì hai góc MSP và PSQ là hai góc kề bù nên suy ra:
góc PSQ = 180o - 50o = 130o.
Hướng dẫn:
a) Trong ∆NML có :
LP ⊥ MN nên LP là đường cao
MQ ⊥ NL nên MQ là đường cao
mà PL ∩ MQ = {S}
suy ra S là trực tâm của tam giác nên đường thằng SN chứa đường cao từ N hay
SN ⊥ ML
b) ∆NMQ vuông tại Q có ˆLNPLNP^ =500 nên ˆQMNQMN^ =400
∆MPS vuông tại Q có ˆQMPQMP^ =400 nên ˆMSPMSP^ =500
Suy ra ˆPSQPSQ^ =1300(kề bù)
a) Trong ∆NML có :
LP ⊥ MN nên LP là đường cao
MQ ⊥ NL nên MQ là đường cao
mà PL ∩ MQ = {S}
suy ra S là trực tâm của tam giác nên đường thằng SN chứa đường cao từ N hay SN ⊥ ML
a) Trong ∆NML có :
LP ⊥ MN nên LP là đường cao
MQ ⊥ NL nên MQ là đường cao
mà PL ∩ MQ = {S}
suy ra S là trực tâm của tam giác nên đường thằng SN chứa đường cao từ N hay
SN ⊥ ML
b) ∆NMQ vuông tại Q có LNP^ =500 nên QMN^ =400
∆MPS vuông tại Q có QMP^ =400 nên MSP^ =500
Suy ra PSQ^ =1300(kề bù)