Căn cứ vào các kí hiệu đã cho trên hình của bài 39 ta có:
ΔABD và ΔACD có:
AB = AC
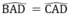
AD là cạnh chung
⇒ ΔABD = ΔACD (c.g.c)
Căn cứ vào các kí hiệu đã cho trên hình của bài 39 ta có:
ΔABD và ΔACD có:
AB = AC
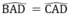
AD là cạnh chung
⇒ ΔABD = ΔACD (c.g.c)
Cho ΔABC cân tại A, đường trung tuyển AD a, Chứng minh ΔABD = ΔACD b, Chứng minh AD BC c, Cho AB = AC = 10cm ; BC = 8cm . Tính AM d, Kẻ trung tuyến CG . Chứng minh DG // AC
Cho hình vẽ: (hình minh họa)
Biết \(\text{ }\widehat{\text{aAB}}\) = \(\widehat{\text{ABC}}\) ; \(\widehat{\text{a'DC}}\) = 60\(^{ }\)độ
a) Chứng minh aa' // bb'
b) Tính số đo \(\widehat{\text{b'Cy'}}\), \(\widehat{\text{DCb'}}\)
c) Gọi Dm là tia phân giác của \(\widehat{\text{a'DC}}\), Cn là tia phân giác của \(\widehat{\text{b'Cy'}}\). Chứng minh Dm//Cn
Cho 2 góc tù Xoy và x'o'y' như hình bẽ bên,trong đó ox//o,x',oy//o'y'.Chứng minh rằng xoy = x'o'y'
Cho hình vẽ sau:
Biết AC ⊥ AB
BD ⊥ AB; góc xCA = 70o
a) Chứng minh rằng AC // BD
b) Tính góc CDB; góc tDq
c) Cx' là tia phân giác của góc yCt. Chứng minh rằng Cx' ⊥ Cy'
Cho tam giác ABC cân tại A, có góc BAC nhọn. Qua A vẽ tia phân giác của góc BAC cắt cạnh BC tại D. a) Chứng minh ΔABD = ΔACD. b) Vẽ đường trung tuyến CF của tam giác ABC cắt cạnh AD tại G. Chứng minh G là trọng tâm của tam giác ABC. c) Gọi H là trung điểm của cạnh DC. Qua H vẽ đường thẳng vuông góc với cạnh DC cắt cạnh AC tại E. Chứng minh ΔDEC cân. d) Chứng minh ba điểm B, G, E thẳng hàng và AD > BD.
Cho tam giác ABC có A B = 3 c m , A C = 4 c m , B C = 5 c m
b. Tia phân giác của góc B cắt AC tại D, H là hình chiếu của D lên BC. Chứng minh Δ A B D = Δ H B D
Bài 2 Cho tam giác nhọn ABC (AB < AC). Gọi M là trung điểm của BC. Trên tia
đối của tia MA lấy điểm D sao cho MD = MA.
a) Chứng minh ABM = DCM.
b) Kẻ AH vuông góc với BC (H BC). Vẽ điểm E sao cho H là trung điểm
của EA. Chứng minh BE = CD.
Bài 3: . Cho ΔABC có AB = AC và D là trung điểm của BC. Gọi E là trung điểm
của AC, trên tia đối của tia EB lấy điểm M sao cho EM = EB.
a) Chứng minh ΔABD = ΔACD
b) Chứng minh rằng AM = 2.BD
c) Tính số đo của ·MAD
Cho tam giác ABC cân tại A, có góc BAC nhọn. Qua A vẽ tia phân giác của góc BAC cắt
cạnh BC tại D.
a) Chứng minh ΔABD = ΔACD.
b) Vẽ đường trung tuyến CF của tam giác ABC cắt cạnh AD tại G. Chứng minh G là trọng
tâm của tam giác ABC.
c) Gọi H là trung điểm của cạnh DC. Qua H vẽ đường thẳng vuông góc với cạnh DC cắt
cạnh AC tại E. Chứng minh ΔDEC cân.
d) Chứng minh ba điểm B, G, E thẳng hàng và AD > BD
Cho tam giác ABC cân tại A, có góc BAC nhọn. Qua A vẽ tia phân giác của góc BAC cắt
cạnh BC tại D.
a) Chứng minh ΔABD = ΔACD.
b) Vẽ đường trung tuyến CF của tam giác ABC cắt cạnh AD tại G. Chứng minh G là trọng
tâm của tam giác ABC.
c) Gọi H là trung điểm của cạnh DC. Qua H vẽ đường thẳng vuông góc với cạnh DC cắt
cạnh AC tại E. Chứng minh ΔDEC cân.
d) Chứng minh ba điểm B, G, E thẳng hàng và AD > BD