Đáp án C
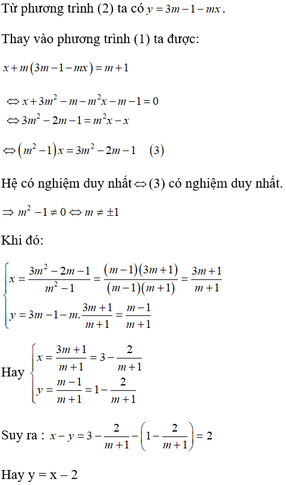
Vậy điểm M(x; y) luôn chạy trên đường thẳng cố định có phương trình y = x - 2
Đáp án C
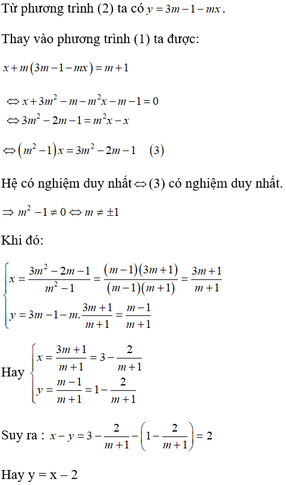
Vậy điểm M(x; y) luôn chạy trên đường thẳng cố định có phương trình y = x - 2
Cho hệ phương trình sau: x+y=2,mx-y=1 b) Tìm m để hệ phương trình có nghiệm duy nhất (x;y) c) Tìm m để hệ phương trình có nghiệm duy nhất (x;y) thỏa mãn x-3y=5 d) Tìm m để hệ phương trình có nghiệm duy nhất (x;y) thỏa mãn xy < 0 e) Tìm m để hệ phương trình có nghiệm duy nhất (x;y) thỏa mãn x+2y > 4 f) Tìm các giá trị của m để x;y là giá trị nguyên
Cho hệ phương trình :
\(\left\{{}\begin{matrix}mx-y=2\\x+my=1\end{matrix}\right.\)
a) Giải hệ phương trình theo tham số m.
b) Trong trường hợp hệ phương trình có nghiệm duy nhất (x, y). Tìm các giá trị của m để x + y = -1.
cho hệ pt
mx+2my=m+1
x+(m+1)y=2
tìm đk của m để hpt có nghiệm duy nhất x,y.
* trong trường hợp đó các điểm M(x;y) luôn thuộc 1 đường thẳng cố định khi m thay đổi
cho hệ pt x-2y=3-m (1) 2x+y=3(m+2) (2) a. giải hệ vs m=2 b. tìm tất các giá trị của m để hệ có nghiệm duy nhất c. tìm GTNN của A=x^2+y^2 trong đó x, y là nghiệm duy nhất của hệ d,. tìm m để hệ có nghiệm sao cho 5x-y=3
cho hệ phương trình
\(\hept{\begin{cases}x-y+m=0\\\left(x+y-2\right)\left(x-2y+1\right)=0\end{cases}}\) (1)
b, với giá trị nào của m, thì hệ phương trình có duy nhất 1 nghiệm
c, tìm m để hệ (1) có 2 nghiệm (x1;y1) và (x2;y2) thỏa mãn x1.x2<0
cho hpt mx+2my và x+(m+1)y=2
a,cmr nếu hệ có nghiệm duy nhất (x,y) thì điểm M(x,y)luôn thuộc 1 đường thẳng cố định khi m thay đổi
b,xác định m để điểm M thuộc góc vuông phần tư thứ nhất
Cho hệ phương trình x + 2 y = 2 m x − y = m . Trong trường hợp hệ phương trình có nghiệm duy nhất (x; y), tìm điều kiện của m để x > 1 và y > 0
A. m > 0
B. m > 1
C. m < −1
D. m > 2
Cho phương trình : \(\left\{{}\begin{matrix}\left(m-1\right)x+y=m\left(1\right)\\x+\left(m-1\right)y=2\left(2\right)\end{matrix}\right.\) có nghiệm duy nhất (x;y)
a) Giải hệ phương trình khi m=3
b) Tìm hệ thức liên hệ giữa x và y ko phụ thuộc vào m
c) Trong trường hợp hệ có nghiệm duy nhất tìm giá trị của m thỏa mãn : 2x2 - 7y = 1
d) Tìm các giá trị của m để biểu thức \(\dfrac{2x-3y}{x+y}\) nhận giá trị nguyên
Bài : Cho hệ phương trình (m + 1)x - y = m + 1 và x + (m -1)y = 2 ( Với m là tham số )
a: Tìm m để hệ phương trình có nghiệm duy nhất (x;y) thỏa mãn x - 2y = 2
b: Tìm các giá trị nguyên của m để hệ phương trình có nghiệm duy nhất (x:y) vơi x,y có giá trị nguyên