Ta có
2 x + 3 y = 7 2 − m 4 x − y = 5 m ⇔ 4 x + 6 y = 7 − 2 m 4 x − y = 5 m ⇔ 7 y = 7 − 7 m 4 x − y = 5 m ⇔ y = 1 − m 4 x − 1 − m = 5 m ⇔ y = 1 − m x = 4 m + 1 4
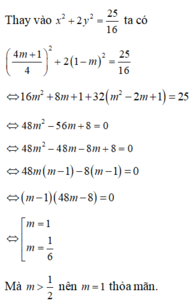
Đáp án: B
Ta có
2 x + 3 y = 7 2 − m 4 x − y = 5 m ⇔ 4 x + 6 y = 7 − 2 m 4 x − y = 5 m ⇔ 7 y = 7 − 7 m 4 x − y = 5 m ⇔ y = 1 − m 4 x − 1 − m = 5 m ⇔ y = 1 − m x = 4 m + 1 4
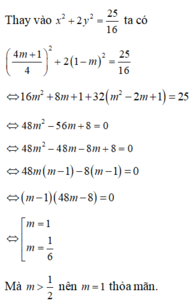
Đáp án: B
bài 1: giải các phương trình sau :
a) x^3-5x=0 b) căn bậc 2 của x-1=3
bài 2 :
cho hệ phương trình : {2x+my;3x-y=0 (I)
a) giải hệ phương trình khi m=0
b) tìm giá trị của m để hệ (I) có nghiệm (x;y) thỏa mãn hệ thức :
x-y+m+1/m-2=-4
bài 3:giải các phương trình sau
a)5x-2/3=5x-3/2 b) 10x+3/12=1+6x+8/9 c) 2(x+3/5)=5-(13/5+x) d) 7/8x-5(x-9)=20x+1,5/6
Bài : Cho hệ phương trình (m + 1)x - y = m + 1 và x + (m -1)y = 2 ( Với m là tham số )
a: Tìm m để hệ phương trình có nghiệm duy nhất (x;y) thỏa mãn x - 2y = 2
b: Tìm các giá trị nguyên của m để hệ phương trình có nghiệm duy nhất (x:y) vơi x,y có giá trị nguyên
Bài 3: Cho hệ phương trình:
\(\left\{{}\begin{matrix}mx-y=1\\2x+my=4\end{matrix}\right.\)
a) Giải hệ khi m=1
b) Tìm tất cả các giá trị của m để hệ phương trình có nghiệm duy nhất (x;y) thỏa mãn x+y=2
cho hệ phương trình
\(\hept{\begin{cases}x-y+m=0\\\left(x+y-2\right)\left(x-2y+1\right)=0\end{cases}}\) (1)
b, với giá trị nào của m, thì hệ phương trình có duy nhất 1 nghiệm
c, tìm m để hệ (1) có 2 nghiệm (x1;y1) và (x2;y2) thỏa mãn x1.x2<0
cho hệ phương trình mx-y=2
3x+my=5( m là tham số)
xác định các giá trị của tham số m để hệ phương trình có nghiệm duy nhất(x;y) thỏa mãn x+y=3/m2+3
a)cho hệ phương trình \(\hept{\begin{cases}x-2y=3-m\\2x+y=3\left(m+2\right)\end{cases}}\)
Gọi nghiệm của hệ phương trình là(x;y)Tìm m để \(x^2+y^2\)đạt GTNN
b)Cho hệ phương trình \(\hept{\begin{cases}mx+y=5\\2x-y=2\end{cases}}\)
Tìm m để hệ phương trình có nghiệm thỏa mãn x+y=1
Cho hệ pt: x+my=9
mx-3y=4
1/ Với giá trị nào của m để hệ có nghiệm (-1;3)
2/ Chứng tỏ răng hệ phương trình luôn luôn có nghiệm duy nhất
3/với giá trị nào của m để nghiêm(x;y) thỏa mãn hệ thức: x-3y=[28/(m^2+3)]-3
Bài 4:Cho phương trình ẩn x: x2 - (m + 3)x + m = 0
a) Chứng minh rằng với mọi giá trị của m phương trình (1) luôn có 2 nghiệm phân biệt.
b) Tìm m để phương trình có 2 nghiệm Phân biệt x1, x2 thỏa mãn hệ thức:
x12 + x22 = 6
Cho hệ phương trình \(\hept{\begin{cases}3x+my=5\\mx-y=2\end{cases}}\). Tìm giá trị của m để phương trình có nghiệm (x;y) thỏa mãn \(x+y=1-\frac{m^2}{m^2+3}\)
cho hệ phương trình \(\left\{{}\begin{matrix}x+y=2\\\left(m+1\right)x+my=7\end{matrix}\right.\)
a) chứng minh rằng: với mọi m thì hệ phương trình luôn có nghiệm x,y thỏa mãn x.y =< 1
b) tìm m là số nguyên để hệ phương trình có nghiệm thỏa mãn x.y>0