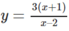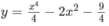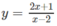Question

Cho hàm số:

a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số.

b) Viết phương trình các đường thẳng đi qua O(0;0) và tiếp xúc với (C) .

c) Tìm tất cả các điểm trên (C) có tọa độ là các số nguyên.

Answer 1

a) Học sinh tự làm

b) Phương trình tiếp tuyến tại điểm M0(x0; y0) là:

y – y0 = y’(x0)(x – x0)

Trong đó:

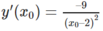
Ta có:

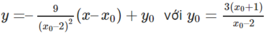
Để đường thẳng đó đi qua O(0; 0), điều kiện cần và đủ là:

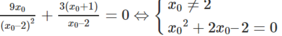
⇔ x0 = –1 - 3 hoặc x0 = –1 +  3

    +) Với x0 = –1 +  3 , ta có phương trình tiếp tuyến:

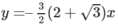
    +) Với x0 = –1 –  3 , ta có phương trình tiếp tuyến:

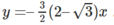
c) Để tìm trên (C) các điểm có tọa độ nguyên ta có:

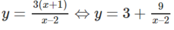
Điều kiện cần và đủ để M(x, y) ∈ (C) có tọa độ nguyên là:

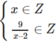
tức (x – 2) là ước của 9.

Khi đó, x – 2 nhận các giá trị -1; 1; -3; 3; -9; 9 hay x nhận các giá trị 1; 3; -1; 5; -7; 11.

Do đó, ta có 6 điểm trên (C) có tọa độ nguyên là: (1;-6), (3;12), (-1;0), (5;6), (-7;2), (11;4).