Question

Cho hàm số \(y=x^3-3mx^2+3.\left(m^2-1\right)x+2024\). Có tất cả bao nhiêu giá trị nguyên của m sao cho hàm số có giá trị nhỏ nhất trên khoảng \(\left(0;+\infty\right)\)

Answer 1

\(y=f\left(x\right)=x^3-3mx^2+3\left(m^2-1\right)x+2024\)

\(f'\left(x\right)=3x^2-6mx+3\left(m^2-1\right)=3.\left(x^2-2mx+m^2-1\right)\)

\(=3\left(x-\left(m+1\right)\right)\left(x-\left(m-1\right)\right)\)

\(f'\left(x\right)=0\Rightarrow\left[{}\begin{matrix}x=m+1\\x=m-1\end{matrix}\right.\)

bbt:

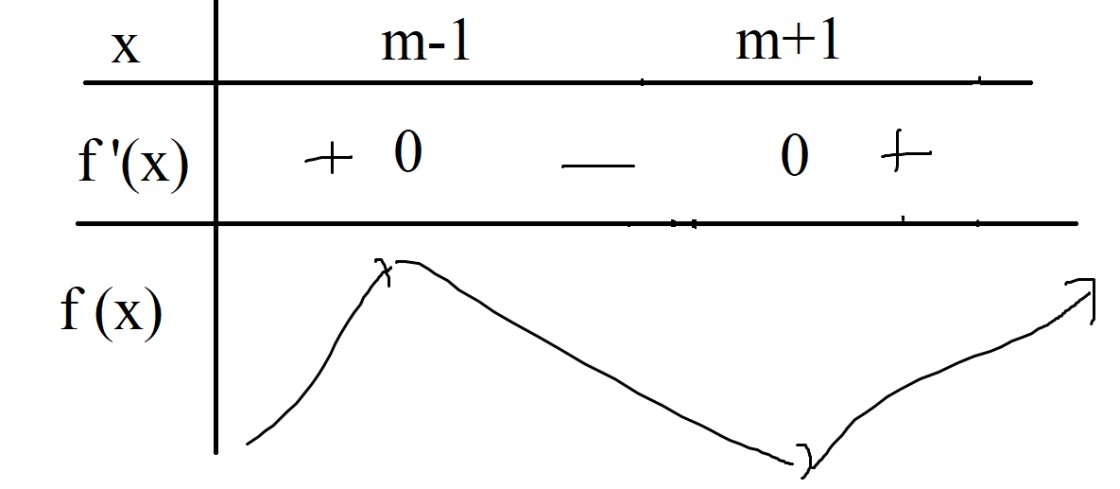
Để hàm số có giá trị nhỏ nhất trên \(\left(0,+\infty\right)\) thì \(m+1>0\Rightarrow m>-1\) và \(f\left(0\right)\ge f\left(m+1\right)\)

\(\Rightarrow2024>m^3-3m-2+2024\Rightarrow m^3-3m-2< 0\)

\(\Rightarrow\left\{{}\begin{matrix}m\le2\\m\ne-1\end{matrix}\right.\)

\(\Rightarrow-1< m\le2\Rightarrow m\in\left\{0,1,2\right\}\)