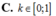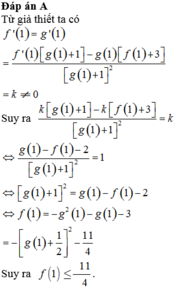Các câu hỏi tương tự
Cho các hàm số y f(x), y g(x),
y
f
(
x
)
+
3
g
(
x
)
+
1
. Hệ số góc tiếp tuyến của các đồ thị hàm số đã cho tại điểm có hoành độ x...
Đọc tiếp
Cho các hàm số y = f(x), y = g(x), y = f ( x ) + 3 g ( x ) + 1 . Hệ số góc tiếp tuyến của các đồ thị hàm số đã cho tại điểm có hoành độ x = 1 bằng nhau và khác 0. Khẳng định nào sau đây là đúng?
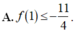
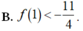
![]()
Cho hàm số yf(x) có đạo hàm tại x1. Gọi d1,d2 lần lượt là tiếp tuyến của đồ thị hàm số yf(x) và yg(x)x . f(2x-1) tại điểm có hoành độ x1 Biết rằng hai đường thẳng d1,d2 vuông góc với nhau. Khẳng định nào dưới đây đúng. A.
f
(
1
)
2
B.
2...
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm tại x=1. Gọi d1,d2 lần lượt là tiếp tuyến của đồ thị hàm số y=f(x) và y=g(x)=x . f(2x-1) tại điểm có hoành độ x=1 Biết rằng hai đường thẳng d1,d2 vuông góc với nhau. Khẳng định nào dưới đây đúng.
A. f ( 1 ) < 2
B. 2 ≤ f ( 1 ) ≤ 2 2
C. 2 ≤ f ( 1 ) ≤ 2
D. f ( 1 ) ≥ 2 2
Cho các hàm số
y
f
x
,
y
g
x
,
y
f
x
+...
Đọc tiếp
Cho các hàm số y = f x , y = g x , y = f x + 3 g x + 1 . Hệ số góc của các tiếp tuyến của các đồ thị các hàm số đã cho tại điểm có hoành độ x = 1 bằng nhau và khác 0. Khẳng định nào dưới đây đúng?
A. f 1 > - 3
B. f 1 < - 3
C. f 1 ≤ - 11 4
D. f 1 ≥ - 11 4
Xét các khẳng định sau: (1) Nếu hàm số yf(x) xác định trên R thỏa mãn f(-1).f(0)0 thì đồ thị của hàm số yf(x) và trục hoành có ít nhất 1 điểm chung. (2) Nếu hàm số yf(x) xác định trên R thỏa mãn f(-1).f(0)0 và f(0).f(1)0 thì đồ thị của hàm số yf(x) và trục hoành có ít nhất 2 điểm chung. Phát biểu nào sau đây đúng? A. Khẳng định đúng và khẳng định sai. B. Khẳng định sai và khẳng định đúng. C. Khẳng định sai và khẳng định sai. D. Khẳng định đúng và khẳng định đúng.
Đọc tiếp
Xét các khẳng định sau:
(1) Nếu hàm số y=f(x) xác định trên R thỏa mãn f(-1).f(0)<0 thì đồ thị của hàm số y=f(x) và trục hoành có ít nhất 1 điểm chung.
(2) Nếu hàm số y=f(x) xác định trên R thỏa mãn f(-1).f(0)<0 và f(0).f(1)<0 thì đồ thị của hàm số y=f(x) và trục hoành có ít nhất 2 điểm chung.
Phát biểu nào sau đây đúng?
A. Khẳng định ![]() đúng và khẳng định
đúng và khẳng định ![]() sai.
sai.
B. Khẳng định ![]() sai và khẳng định
sai và khẳng định ![]() đúng.
đúng.
C. Khẳng định ![]() sai và khẳng định
sai và khẳng định ![]() sai.
sai.
D. Khẳng định ![]() đúng và khẳng định
đúng và khẳng định ![]() đúng.
đúng.
Cho hàm số y f(x) có
1
≤
f
(
x
)
≤
4
với mọi
x
∈
2
;
5
. Hỏi khẳng định nào dưới đây là khẳng định đúng? A.
3
≤
f
(
5
)
-
f
(
2
)
≤
12
B.
-
12
≤...
Đọc tiếp
Cho hàm số y = f(x) có 1 ≤ f ' ( x ) ≤ 4 với mọi x ∈ 2 ; 5 . Hỏi khẳng định nào dưới đây là khẳng định đúng?
A. 3 ≤ f ( 5 ) - f ( 2 ) ≤ 12
B. - 12 ≤ f ( 5 ) - f ( 2 ) ≤ 3
C. 1 ≤ f ( 5 ) - f ( 2 ) ≤ 4
D. - 4 ≤ f ( 5 ) - f ( 2 ) ≤ - 1
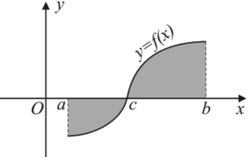
Cho hàm số y f(x) liên tục trên đoạn [a;b] và cắt trục hoành tại điểm x c (như hình vẽ). Gọi S là diện tích hình phẳng được giới hạn bởi đồ thị của hàm số y f(x), trục hoành và hai đường thẳng x a, x b. Khẳng định nào sau đây là khẳng định đúng?
Đọc tiếp
Cho hàm số y = f(x) liên tục trên đoạn [a;b] và cắt trục hoành tại điểm x = c (như hình vẽ). Gọi S là diện tích hình phẳng được giới hạn bởi đồ thị của hàm số y = f(x), trục hoành và hai đường thẳng x = a, x = b. Khẳng định nào sau đây là khẳng định đúng?
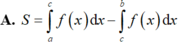
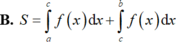
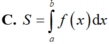
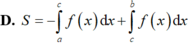
Cho hàm số y f(x) có đạo hàm đến cấp hai liên tục trên R. Biết rằng các tiếp tuyến với đồ thị y f(x) tại các điểm có hoành độ x -1, x 0, x 1 lần lượt tạo với chiều dương của trục Ox các góc
30
o
,
45
o
,
60
o
Tính tích phân
I
∫
-
1
0
f...
Đọc tiếp
Cho hàm số y = f(x) có đạo hàm đến cấp hai liên tục trên R. Biết rằng các tiếp tuyến với đồ thị y = f(x) tại các điểm có hoành độ x = -1, x = 0, x = 1 lần lượt tạo với chiều dương của trục Ox các góc 30 o , 45 o , 60 o
Tính tích phân I = ∫ - 1 0 f ' x . f ' ' x dx + 4 ∫ 0 1 f ' x 3 . f ' ' x dx .
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Cho hàm số y f(x) có đạo hàm đến cấp hai liên tục trên R. Biết rằng các tiếp tuyến với đồ thị y f(x) tại các điểm có hoành độ x -1, x0, x1 lần lượt tạo với chiều dương của trục Ox các góc
30
o
,
45
o
,
60
o
Tính tích phân
I
∫
-
1
0
f...
Đọc tiếp
Cho hàm số y = f(x) có đạo hàm đến cấp hai liên tục trên R. Biết rằng các tiếp tuyến với đồ thị y = f(x) tại các điểm có hoành độ x = -1, x=0, x=1 lần lượt tạo với chiều dương của trục Ox các góc 30 o , 45 o , 60 o
Tính tích phân I = ∫ - 1 0 f ' x . f ' ' x dx + 4 ∫ 0 1 f ' x 3 . f ' ' x dx .
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Cho hàm số yf(x) có đạo hàm xác định và liên tục trên Rvới
y
f
(
x
)
x
3
-
x
2
-
2
x
. Gọi k là hệ số góc của đường thẳng đi qua hai điểm cực tiểu của đồ thị hàm số yf(x). Khẳng định nào sau đây đúng ?
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm xác định và liên tục trên Rvới y = f ' ( x ) = x 3 - x 2 - 2 x . Gọi k là hệ số góc của đường thẳng đi qua hai điểm cực tiểu của đồ thị hàm số y=f(x). Khẳng định nào sau đây đúng ?
![]()
![]()