không đổi khi và chỉ khi 
.
đồng biến khi và chỉ khi 
và 
tại hữu hạn giá trị 
nghịch biến khi và chỉ khi 
.
Các câu hỏi tương tự
Cho hàm số
f
x
a
x
3
+
b
x
2
+
c
x
+
d
với
a
,
b
,...
Đọc tiếp
Cho hàm số f x = a x 3 + b x 2 + c x + d với a , b , c , d là các hệ số thực và a ≠ 0 . Hàm số f x nghịch biến trên ℝ khi và chỉ khi:
A. a < 0 b 2 ≤ 3 a c
B. a < 0 b 2 < 3 a c
C. a > 0 b 2 ≥ 3 a c
D. a > 0 b 2 < 3 a c
Cho hàm số liên tục trên khoảng (a;b) và
x
0
∈
(
a
;
b
)
.
Có bao nhiêu mệnh đề đúng trong các mệnh đề sau?(1) Hàm số đạt cực trị tại điểm
x
0
khi và chỉ khi
f
(
x
0
)
0
.
(2) Nếu hàm số
y
f
(
x
)
có đạo hàm và có đạo...
Đọc tiếp
Cho hàm số liên tục trên khoảng (a;b) và x 0 ∈ ( a ; b ) . Có bao nhiêu mệnh đề đúng trong các mệnh đề sau?
(1) Hàm số đạt cực trị tại điểm x 0 khi và chỉ khi f ' ( x 0 ) = 0 .
(2) Nếu hàm số y = f ( x ) có đạo hàm và có đạo hàm cấp hai tại điểm x 0 thỏa mãn điều kiện f ' ( x 0 ) = f ' ' ( x 0 ) = 0 thì điểm x 0 không phải là điểm cực trị của hàm số y = f ( x ) .
(3) Nếu f'(x) đổi dấu khi x qua điểm x 0 thì điểm x 0 là điểm cực tiểu của hàm số y = f ( x ) .
(4) Nếu hàm số y = f ( x ) có đạo hàm và có đạo hàm cấp hai tại điểm x 0 thỏa mãn điều kiện f ' ( x 0 ) = 0 , f ' ' ( x 0 ) > 0 thì điểm x 0 là điểm cực tiểu của hàm số y = f ( x ) .
A. 1
B. 2
C. 0
D. 3
Cho hàm số y f(x) có đạo hàm trên R và có bảng biến thiên như hình bên Phương trình f(x) m có hai nghiệm thực phân biệt khi và chỉ khi
Đọc tiếp
Cho hàm số y = f(x) có đạo hàm trên R và có bảng biến thiên như hình bên
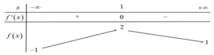
Phương trình f(x) = m có hai nghiệm thực phân biệt khi và chỉ khi
Cho hàm số y f(x). Hàm số y f(x) có bảng biến thiên như sau Bất phương trình
f
(
x
)
e
x
+
m
đúng với mọi
x
∈
-
1
;
1
khi và chỉ khi
Đọc tiếp
Cho hàm số y = f(x). Hàm số y = f'(x) có bảng biến thiên như sau
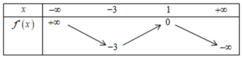
Bất phương trình f ( x ) < e x + m đúng với mọi x ∈ - 1 ; 1 khi và chỉ khi
Cho hàm số y f(x).Hàm số y f’(x) có bảng biến thiên như sau Bất phương trình
f
(
x
)
e
x
+
m
đúng với mọi
x
∈
(
-
1
;
1
)
khi và chỉ khi A. B. C. D.
Đọc tiếp
Cho hàm số y= f(x).Hàm số y= f’(x) có bảng biến thiên như sau
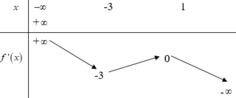
Bất phương trình f ( x ) < e x + m đúng với mọi x ∈ ( - 1 ; 1 ) khi và chỉ khi
A.
B. 
C. 
D. 
Cho hàm số y f(x).Hàm số y f’(x) có bảng biến thiên như sau Bất phương trình
f
(
e
x
)
e
x
+
m
nghiệm đúng với mọi
x
∈
(
-
1
;
1
)
khi và chỉ khi A. B. C. D.
Đọc tiếp
Cho hàm số y= f(x).Hàm số y= f’(x) có bảng biến thiên như sau
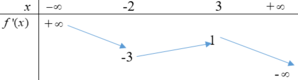
Bất phương trình f ( e x ) < e x + m nghiệm đúng với mọi x ∈ ( - 1 ; 1 ) khi và chỉ khi
A.
B. 
C. 
D. 
Cho hàm số yf(x). Hàm số f(x) có biến thiên Bất phương trình f(sin x) -3x + m đúng với mọi
x
∈
-
π
2
;
π
2
khi và chỉ khi A.
m
≥
f
(
1
)
+
3
π...
Đọc tiếp
Cho hàm số y=f(x). Hàm số f'(x) có biến thiên
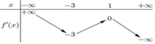
Bất phương trình f(sin x)< -3x + m đúng với mọi x ∈ - π 2 ; π 2 khi và chỉ khi
A. m ≥ f ( 1 ) + 3 π 2
B. m > f ( - 1 ) - 3 π 2
C. m > f ( π 2 ) + 3 π 2
D. m > f ( 1 ) + 3 π 2
Cho hàm số y f(x).Hàm số y f’(x) có bảng biến thiên như sau Bất phương trình
m
+
e
f
(
x
)
e
x
có nghiệm khi và chỉ khi A. B. C. D.
Đọc tiếp
Cho hàm số y= f(x).Hàm số y= f’(x) có bảng biến thiên như sau
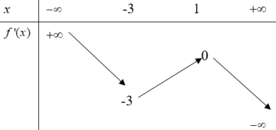
Bất phương trình
m
+
e
f
(
x
)
<
e
x
có nghiệm 
khi và chỉ khi
A. 
B. 
C. 
D. 
Hàm số
y
x
3
+
m
x
-
1
đồng biến trên R khi và chỉ khi A.
m
≥
0
B. m 0 C.
m
≤
0
D. m 0
Đọc tiếp
Hàm số y = x 3 + m x - 1 đồng biến trên R khi và chỉ khi
A. m ≥ 0
B. m > 0
C. m ≤ 0
D. m < 0
Cho các phát biểu sau: I. Đồ thị hàm số có y x4 – x + 2 có trục đối xứng là Oy. II. Hàm số f(x) liên tục và có đạo hàm trên khoảng (a;b) đạt cực trị tại điểm x0 thuộc khoảng (a;b) thì tiếp tuyến tại điểm M(x0,f(x0)) song song với trục hoành. III. Nếu f(x) nghịch biến trên khoảng (a;b) thì hàm số không có cực trị trên khoảng (a;b). IV. Hàm số f(x) xác định và liên tục trên khoảng (a;b) và đạt cực tiểu tại điểm x0 thuộc khoảng (a;b) thì f(x) nghịch biến trên khoảng (a;x0) và đồng biến trên khoảng...
Đọc tiếp
Cho các phát biểu sau:
I. Đồ thị hàm số có y = x4 – x + 2 có trục đối xứng là Oy.
II. Hàm số f(x) liên tục và có đạo hàm trên khoảng (a;b) đạt cực trị tại điểm x0 thuộc khoảng (a;b) thì tiếp tuyến tại điểm M(x0,f(x0)) song song với trục hoành.
III. Nếu f(x) nghịch biến trên khoảng (a;b) thì hàm số không có cực trị trên khoảng (a;b).
IV. Hàm số f(x) xác định và liên tục trên khoảng (a;b) và đạt cực tiểu tại điểm x0 thuộc khoảng (a;b) thì f(x) nghịch biến trên khoảng (a;x0) và đồng biến trên khoảng (x0;b).
Các phát biểu đúng là:
A. II,III,IV
B. I,II,III
C. III,IV
D. I,III,IV