Theo bài toán ta có thể suy ra BBT của đồ thị hàm số y = f (x) như sau:
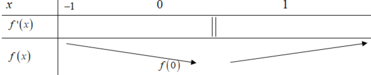
Dễ thấy trong các đáp án A, C, D đều sai. Hàm số đạt cực tiểu tại x = 0.
Chọn B
Cho hàm số y = x 3 - 3 x 2 có giá trị lớn nhất và giá trị nhỏ nhất trên đoạn [-2;1] lần lượt là M và m. Tính T = M + m.
A. T = -20
B. T = -4
C. T = -22
D. T = 2
Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y= x 2 + x + 3 x - 2 trên [-2;1] . Tính T=M+2m .
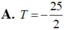
Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số 
trên [-2;1] . Tính T =M + 2m .
A. 
B. 
C. 
D. 
Cho hàm số y = f(x) có đồ thị như hình vẽ. Gọi giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn [-2;1] lần lượt là M, m. Giá trị M + m bằng
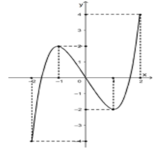
A. 2
B. -2
C. 0
D. 4
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = - x 4 + x 2 - 1 trên đoạn [-2;1]. Tính M + m.
A. 0.
B. -9.
C. -10.
D. -1.
Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x)= x^3-3x^2+2 trên đoạn [-1,2] . Tính giá trị biểu thức P= M-2m A. 3√2-3 B. 2√2-5 C. 3√3-5 D. 3√3-3
Cho hàm số y=f(x) liên tục trên [-3;2] và có bảng biến thiên như sau. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y=f(x) trên đoạn [-1;2]. Tính M + m.
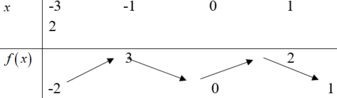
A. 3
B. 2
C. 1
D. 4
Kí hiệu m, M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = x + 3 2 x - 1 trên đoạn [1;4]. Tính giá trị biểu thức d = M – m
A. d = 3
B. d = 4
C. d = 5
D. d = 2
Cho hàm số y = f(x) liên tục trên đoạn [-2;2] và có đồ thị như hình vẽ dưới đây. Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên đoạn [-2;2]. Tính M+m.
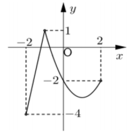
A. -1
B. -2
C. 0
D. -3
