Các câu hỏi tương tự
Cho hàm số
y
a
x
4
+
b
x
2
+
c
có đồ thị (C) biết rằng (C) đi qua điểm A(-1;0) tiếp tuyến d tại A của (C) cắt (C) tại hai điểm có hoành độ lần lượt là 0 và 2, diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x0; x2 có diện tích bằng 28/5 (phần gạch chéo trong hình vẽ). Diện tích hình phẳng giới hạn bởi d, đồ thị (C) và...
Đọc tiếp
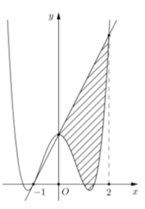
Cho hàm số y = a x 4 + b x 2 + c có đồ thị (C) biết rằng (C) đi qua điểm A(-1;0) tiếp tuyến d tại A của (C) cắt (C) tại hai điểm có hoành độ lần lượt là 0 và 2, diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x=0; x=2 có diện tích bằng 28/5 (phần gạch chéo trong hình vẽ). Diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x=-1; x = 0 có diện tích bằng:
A. 2/5
B. 1/9
C. 2/9
D. 1/5
Cho hàm số có đồ thị (C)
y
2
x
+
1
x
-
1
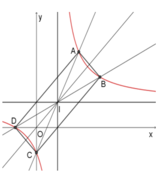
và đường thẳng d: yx+m. Đường thẳng d cắt đồ thị (C) tại hai điểm A và B. Với C( -2; 5) , giá trị của tham số m để tam giác ABC đều là A.m1 B.m1 hoặc m5 C.m5 D.m-5
Đọc tiếp
Cho hàm số có đồ thị (C) y = 2 x + 1 x - 1 và đường thẳng d: y=x+m. Đường thẳng d cắt đồ thị (C) tại hai điểm A và B. Với C( -2; 5) , giá trị của tham số m để tam giác ABC đều là
A.m=1
B.m=1 hoặc m=5
C.m=5
D.m=-5
Cho (C) là đồ thị của hàm số y(x-2)/(x+1) và đường thẳng d:ymx+1. Tìm các giá trị thực của tham số m để đường thẳng d cắt đồ thị hàm số (C) tại hai điểm A,B phân biệt thuộc hai nhánh khác nhau của (C) A. B. C. D.
Đọc tiếp
Cho (C) là đồ thị của hàm số y=(x-2)/(x+1) và đường thẳng d:y=mx+1. Tìm các giá trị thực của tham số m để đường thẳng d cắt đồ thị hàm số (C) tại hai điểm A,B phân biệt thuộc hai nhánh khác nhau của (C)
A.![]()
B.![]()
C.![]()
D. ![]()
Cho hàm số
y
a
x
4
+
b
x
2
+
c
có đồ thị (C) biết rằng (C) đi qua điểm A(-1;0) tiếp tuyến d tại A của A cắt (C) tại 2 điểm có hoành độ lần lượt là 0 và 2, diện tích hình phẳng giới hạn bởi d, đồ thị (C) và 2 đường thẳng x0; x2 có diện tích bằng 28/5 (phần gạch chéo trong hình vẽ).Diện tích hình phẳng giới hạn bởi d, đồ thị (C) và 2 đường thẳn...
Đọc tiếp
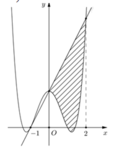
Cho hàm số y = a x 4 + b x 2 + c có đồ thị (C) biết rằng (C) đi qua điểm A(-1;0) tiếp tuyến d tại A của A cắt (C) tại 2 điểm có hoành độ lần lượt là 0 và 2, diện tích hình phẳng giới hạn bởi d, đồ thị (C) và 2 đường thẳng x=0; x=2 có diện tích bằng 28/5 (phần gạch chéo trong hình vẽ).Diện tích hình phẳng giới hạn bởi d, đồ thị (C) và 2 đường thẳng x = 0; x=2 có diện tích bằng
A. 2/5
B. 1/9
C. 2/9
D. 1/5
Cho hàm số: y x3+2mx2+3(m-1)x+2 có đồ thị (C) . Đường thẳng d: y - x+2 cắt đồ thị (C) tại ba điểm phân biệt A(0; -2); B và C. Với M(3;1) giá trị của tham số m để tam giác MBC có diện tích bằng
2
7
là A. m-1 B. m-1 hoặc m4 C. m4 D. Không tồn tại m
Đọc tiếp
Cho hàm số: y = x3+2mx2+3(m-1)x+2 có đồ thị (C) . Đường thẳng d: y= - x+2 cắt đồ thị (C) tại ba điểm phân biệt A(0; -2); B và C. Với M(3;1) giá trị của tham số m để tam giác MBC có diện tích bằng 2 7 là
A. m=-1
B. m=-1 hoặc m=4
C. m=4
D. Không tồn tại m
Đồ thị hàm số y f(x) đối xứng với đồ thị của hàm số
y
a
x
(
a
0
,
a
≠
1
)
qua điểm I(1;1). Giá trị của biểu thức
2
+
log
a
1
2018
bằng
Đọc tiếp
Đồ thị hàm số y = f(x) đối xứng với đồ thị của hàm số y = a x ( a > 0 , a ≠ 1 ) qua điểm I(1;1). Giá trị của biểu thức 2 + log a 1 2018 bằng
![]()
![]()
![]()
![]()
Cho hàm số
y
x
-
x
+
1
có đồ thị, đường thẳng (d): y mx-m-1 và điểm A(-1;0) Biết đường thẳng d cắt đồ thị tại hai điểm phân biệt M, N mà
AM
2
+
AN...
Đọc tiếp
Cho hàm số y = x - x + 1 có đồ thị, đường thẳng (d): y = mx-m-1 và điểm A(-1;0) Biết đường thẳng d cắt đồ thị tại hai điểm phân biệt M, N mà AM 2 + AN 2 đạt giá trị nhỏ nhất. Mệnh đề nào dưới đây đúng?
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Cho hai hàm số
f
(
x
)
a
x
3
+
b
x
2
+
c
x
-
1
2
và
g
(
x
)
d
x
2
+
e
x
+
1
(
a
,
b
,
c
,
d...
Đọc tiếp
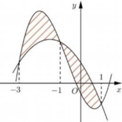
Cho hai hàm số f ( x ) = a x 3 + b x 2 + c x - 1 2 và g ( x ) = d x 2 + e x + 1 ( a , b , c , d , e ∈ ℝ ) . Biết rằng đồ thị của hàm số y = f(x) và y = g(x) cắt nhau tại ba điểm có hoành độ lần lượt là –3; –1;1 (tham khảo hình vẽ). Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng
A. 9 2
B. 8
C. 4
D. 5
Cho hàm số
y
x
3
-
3
x
2
+
4
có đồ thị (C) , đường thẳng (d): ym(x+1) với m là tham số, đường thẳng
∆
:
y
2
x
-
7
. Tìm tổng tất cả các giá trị của tham số m để đường thẳng (d) cắt đồ thị (C) tại 3 điểm phân biệt A(-1;0); B;C sao cho B,C cùng phía với
∆
và...
Đọc tiếp
Cho hàm số y = x 3 - 3 x 2 + 4 có đồ thị (C) , đường thẳng (d): y=m(x+1) với m là tham số, đường thẳng ∆ : y = 2 x - 7 . Tìm tổng tất cả các giá trị của tham số m để đường thẳng (d) cắt đồ thị (C) tại 3 điểm phân biệt A(-1;0); B;C sao cho B,C cùng phía với ∆ và d B ; ∆ + d C ; ∆ = 6 5 .
A. 0
B. 8
C. 5
D. 4