Các câu hỏi tương tự
Cho hàm số
y
x
-
2
x
+
1
có đồ thị (C) . Phương trình tiếp tuyến
∆
của đồ thị hàm số (C) tạo với hai đường tiệm cận một tam giác có bán kính đường tròn nội tiếp lớn nhất. Khi đó, khoảng cách từ tâm đối xứng của đồ thị đến
∆
bằng?
A
....
Đọc tiếp
Cho hàm số y = x - 2 x + 1 có đồ thị (C) . Phương trình tiếp tuyến ∆ của đồ thị hàm số (C) tạo với hai đường tiệm cận một tam giác có bán kính đường tròn nội tiếp lớn nhất. Khi đó, khoảng cách từ tâm đối xứng của đồ thị đến ∆ bằng?
A . 3
B . 2 6
C . 2 3
D . 6
Cho hàm số
y
x
+
1
x
-
2
(C). Gọi d là khoảng cách từ giao điểm của hai đường tiệm cận của đồ thị đến một tiếp tuyến của (C). Giá trị lớn nhất mà d có thể đạt được là: A. B. . C. . D. .
Đọc tiếp
Cho hàm số y = x + 1 x - 2 (C). Gọi d là khoảng cách từ giao điểm của hai đường tiệm cận của đồ thị đến một tiếp tuyến của (C). Giá trị lớn nhất mà d có thể đạt được là:
A. ![]()
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Cho hàm số
y
f
(
x
)
a
x
4
+
b
x
2
+
c
có đồ thị như hình bên dưới. Tìm tổng tất cả các đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
y
x
(
x
-
1
)
f...
Đọc tiếp
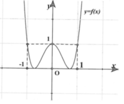
Cho hàm số
y
=
f
(
x
)
=
a
x
4
+
b
x
2
+
c
có đồ thị như hình bên dưới. Tìm tổng tất cả các đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
y
=
x
(
x
-
1
)
f
(
x
)
-
1
![]()
![]()
![]()
![]()
Cho hàm số
y
x
+
1
a
x
2
+
1
có đồ thị (C). Biết rằng (C) có tiệm cận ngang và tồn tại tiếp tuyến của (C) song song và cách tiệm cận ngang của (C) một khoảng bằng 3. Mệnh đề nào dưới đây đúng ?
Đọc tiếp
Cho hàm số y = x + 1 a x 2 + 1 có đồ thị (C). Biết rằng (C) có tiệm cận ngang và tồn tại tiếp tuyến của (C) song song và cách tiệm cận ngang của (C) một khoảng bằng 3. Mệnh đề nào dưới đây đúng ?
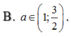
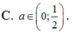
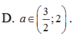
Cho hàm số
y
x
+
2
1
-
x
2
. Xét các mệnh đề sau đây: (I). Hàm số có tập xác định D(-1;1). (II). Đồ thị hàm số có 2 đường tiệm cận ngang là y1 và y-1. (III). Đồ thị hàm số có 2 đường tiệm cận đứng là x1 và x-1...
Đọc tiếp
Cho hàm số y = x + 2 1 - x 2 . Xét các mệnh đề sau đây:
(I). Hàm số có tập xác định D=(-1;1).
(II). Đồ thị hàm số có 2 đường tiệm cận ngang là y=1 và y=-1.
(III). Đồ thị hàm số có 2 đường tiệm cận đứng là x=1 và x=-1.
(IV). Hàm số có một cực trị.
Số mệnh đề đúng là:
A.3
B.1
C.2
D.4
Cho hàm số
y
x
-
2
m
x
2
-
2
x
+
4
. Có tất cả bao nhiêu giá trị của tham số m để đồ thị hàm số có đúng hai đường tiệm cận (tiệm cận đứng và tiệm cận ngang)? A. 1. B. 3. C. 0. D. 2.
Đọc tiếp
Cho hàm số y = x - 2 m x 2 - 2 x + 4 . Có tất cả bao nhiêu giá trị của tham số m để đồ thị hàm số có đúng hai đường tiệm cận (tiệm cận đứng và tiệm cận ngang)?
A. 1.
B. 3.
C. 0.
D. 2.
Biết rằng đồ thị hàm số y = a x + 1 b x - 2 có đường tiệm cận đứng là x = 2 và đường tiệm cận ngang là y = 3. Tính giá trị của a + b?
A. 1.
B. 5.
C. 4.
D. 0.
Cho hàm số
y
2
x
+
1
x
-
1
có đồ thị (C) . Gọi I là giao điểm của hai tiệm cận. Tiếp tuyến của (C) cắt 2 tiệm cận tại A và B sao cho chu vi tam giác IAB đạt giá trị nhỏ nhất. Khoảng cách lớn nhất từ gốc tọa độ đến tiếp tuyến
∆
gần giá trị nào nhất? A. 6. B. 4. C. 3. D. 5.
Đọc tiếp
Cho hàm số y = 2 x + 1 x - 1 có đồ thị (C) . Gọi I là giao điểm của hai tiệm cận. Tiếp tuyến của (C) cắt 2 tiệm cận tại A và B sao cho chu vi tam giác IAB đạt giá trị nhỏ nhất. Khoảng cách lớn nhất từ gốc tọa độ đến tiếp tuyến ∆ gần giá trị nào nhất?
A. 6.
B. 4.
C. 3.
D. 5.
Cho hàm số
y
x
+
2
x
+
1
có đồ thị là (C). Gọi d là khoảng cách từ giao điểm 2 tiệm cận của (C) đến một tiếp tuyến bất kỳ của (C). Giá trị lớn nhất d có thể đạt được là: A. . B. . C. . D. .
Đọc tiếp
Cho hàm số y = x + 2 x + 1 có đồ thị là (C). Gọi d là khoảng cách từ giao điểm 2 tiệm cận của (C) đến một tiếp tuyến bất kỳ của (C). Giá trị lớn nhất d có thể đạt được là:
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.