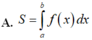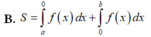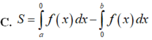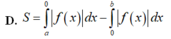Các câu hỏi tương tự
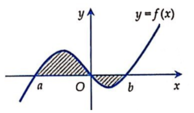
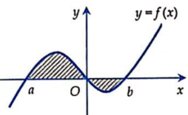
Cho hàm số yf(x) có đồ thị hình bên thì công thức tính diện tích hình phẳng phần tô đậm trong hình là: A.
S
∫
a
b
f
x
d
x
B.
S
∫
a
0
f
x
d
x
+
∫
0
b
f
x
d
x
C...
Đọc tiếp
Cho hàm số y=f(x) có đồ thị hình bên thì công thức tính diện tích hình phẳng phần tô đậm trong hình là:
A. S = ∫ a b f x d x
B. S = ∫ a 0 f x d x + ∫ 0 b f x d x
C. S = ∫ a 0 f x d x − ∫ 0 b f x d x
D. S = ∫ a 0 f x d x − ∫ 0 b f x d x
Cho đồ thị hàm số y f(x) . Diện tích S của hình phẳng (phần tô đen trong hình vẽ) được tính theo công thức dưới đây?
Đọc tiếp
Cho đồ thị hàm số y = f(x) . Diện tích S của hình phẳng (phần tô đen trong hình vẽ) được tính theo công thức dưới đây?
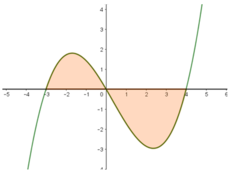

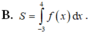
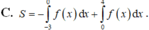
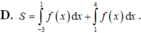
Trên mặt phẳng tọa độ Oxy, cho phần hình phẳng được tô đậm như hình bên được giới hạn bởi một đồ thị hàm số bậc ba đa thức và một đường thẳng. Diện tích S của phần tô đậm đó bằng bao nhiêu? A. S 8 B. S 6 C. S 2 D. S 4
Đọc tiếp
Trên mặt phẳng tọa độ Oxy, cho phần hình phẳng được tô đậm như hình bên được giới hạn bởi một đồ thị hàm số bậc ba đa thức và một đường thẳng. Diện tích S của phần tô đậm đó bằng bao nhiêu?
A. S = 8
B. S = 6
C. S = 2
D. S = 4
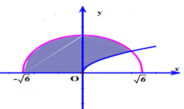
Gọi H là hình phẳng giới hạn bởi đồ thị hàm số
y
x
, cung tròn có phương trình
y
6
-
x
2
(
-
6
≤
x
≤
6
)
và trục hoành (phần tô đậm trong hình vẽ bên). Tính thể tích V của vật thể tròn xoay sinh bởi khi quay hình phẳng H quanh trục
Đọc tiếp
Gọi H là hình phẳng giới hạn bởi đồ thị hàm số y = x , cung tròn có phương trình y = 6 - x 2 ( - 6 ≤ x ≤ 6 ) và trục hoành (phần tô đậm trong hình vẽ bên). Tính thể tích V của vật thể tròn xoay sinh bởi khi quay hình phẳng H quanh trục
![]()
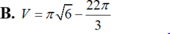
![]()
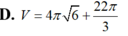
Cho hàm số
f
(
x
)
a
x
4
+
b
x
2
(
a
,
b
∈
ℝ
)
có đồ thị hàm số f(x) như hình vẽ bên dưới. Biết rằng diện tích phần tô đậm bằng
1
8
. Phương trình 8f(x) + 1 0 có bao nhiêu nghiệm? A. 0 B. 4 C. 3...
Đọc tiếp
Cho hàm số f ( x ) = a x 4 + b x 2 ( a , b ∈ ℝ ) có đồ thị hàm số f'(x) như hình vẽ bên dưới. Biết rằng diện tích phần tô đậm bằng 1 8 . Phương trình 8f(x) + 1 = 0 có bao nhiêu nghiệm?
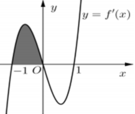
A. 0
B. 4
C. 3
D. 2
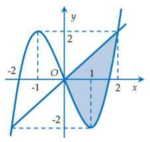
Cho hàm số y f(x) liên tục trên Rvà có đồ thị như hình vẽ bên. Hình phẳng được đánh dấu trong hình bên có diện tích là
Đọc tiếp
Cho hàm số y = f(x) liên tục trên Rvà có đồ thị như hình vẽ bên. Hình phẳng được đánh dấu trong hình bên có diện tích là
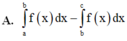
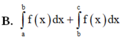
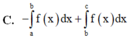
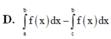
Cho đồ thị hàm số yf(x) Diện tích hình phẳng (phần có dấu gạch trong hình) là
Đọc tiếp
Cho đồ thị hàm số y=f(x) Diện tích hình phẳng (phần có dấu gạch trong hình) là
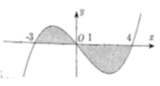
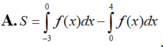
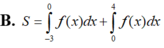
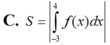
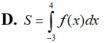
Cho đồ thị hàm số y f(x). Diện tích hình phẳng (phần có đánh dấu gạch trong hình) là: A.
∫
-
3
0
f
x
d
x
+
∫
4
0
f
x
d
x
B.
∫
-
3
1
f
x
d...
Đọc tiếp
Cho đồ thị hàm số y = f(x). Diện tích hình phẳng (phần có đánh dấu gạch trong hình) là:
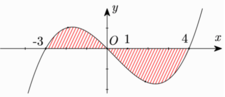
A. ∫ - 3 0 f x d x + ∫ 4 0 f x d x
B. ∫ - 3 1 f x d x + ∫ 1 4 f x d x
C. ∫ 0 - 3 f x d x + ∫ 0 4 f x d x
D. ∫ - 3 4 f x d x
Cho đồ thị hàm số
y
f
(
x
)
.
Diện tích hình phẳng (phần có đánh dấu gạch trong hình) là: A.
∫
-
3
0
f
x
d
x
+
∫
4
0
f
x
d
x
B.
∫
-...
Đọc tiếp
Cho đồ thị hàm số y = f ( x ) . Diện tích hình phẳng (phần có đánh dấu gạch trong hình) là:
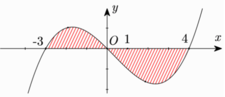
A. ∫ - 3 0 f x d x + ∫ 4 0 f x d x
B. ∫ - 3 1 f x d x + ∫ 1 4 f x d x
C. ∫ 0 - 3 f x d x + ∫ 0 4 f x d x
D. ∫ - 3 4 f x d x