Chọn C.
Dựa vào đồ thị hàm số f'(x) ta thấy
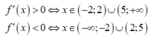
Xét hàm số y = f(3-2x) có y' = -2.f'(3-2x)
Hàm số y = f(3-2x) nghịch biến ![]()
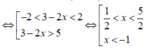
Vậy hàm số y = f(3-2x) nghịch biến trên các khoảng 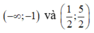
Chọn C.
Dựa vào đồ thị hàm số f'(x) ta thấy
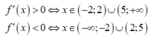
Xét hàm số y = f(3-2x) có y' = -2.f'(3-2x)
Hàm số y = f(3-2x) nghịch biến ![]()
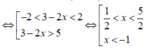
Vậy hàm số y = f(3-2x) nghịch biến trên các khoảng 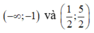
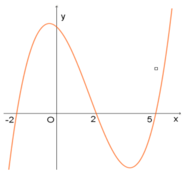
Cho hàm số f (x) Đồ thị hàm số y=f'(x) như hình vẽ bên. Hàm số g(x)=f(3-2x) nghịch biến trên khoảng nào trong các khoảng sau?
A.![]()
B.![]()
C.![]()
D.![]()
Cho hàm số f (x) Đồ thị hàm số y=f'(x) như hình vẽ bên. Hàm số g(x)=f(2-3x) nghịch biến trên khoảng nào trong các khoảng sau?

![]()
![]()
![]()
![]()
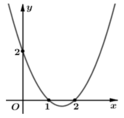
Cho hàm số y= f(x) . Đồ thị hàm số y= f’(x) như hình bên. Hỏi hàm số y= g(x) = f(1-x2) nghịch biến trên khoảng nào trong các khoảng sau?
A. (1; 2)
B. (0; + ∞)
C. (-2; -1)
D. (-1; 1)
Cho hàm số y= f( x) Đồ thị hàm số y= f'x như hình bên dưới
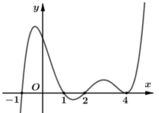
Hàm số y= g( x) = f( 1-2x) đồng biến trên khoảng nào trong các khoảng sau?
A. (-1; 0)
B. (-∞;0)
C. (0; 1)
D. ( 1; + ∞)
Cho hàm số y=f(x). Hàm số y=f'(x) có đồ thị như hình bên. Hàm số y = f ( 1 + x 2 ) nghịch biến trên khoảng nào dưới đây?
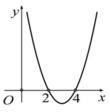
![]()
![]()
![]()
![]()
Cho hàm số y= f( x) có đạo hàm là hàm số f’(x) trên R. Biết rằng hàm số ![]() có đồ thị như hình vẽ bên dưới. Hàm số y= f(x) nghịch biến trên khoảng nào?
có đồ thị như hình vẽ bên dưới. Hàm số y= f(x) nghịch biến trên khoảng nào?

A. (-3; -1) và (1; 3).
B. (-1; 1) và (3; 5).
C. ![]() .
.
D. (- 5; -3) và (-1; 1).
Cho hàm số y=f(x) liên tục trên đoạn [-1;4] và có đồ thị hàm số y=f’(x) như hình bên. Hỏi hàm số g ( x ) = f x 2 + 1 nghịch biến trên khoảng nào trong các khoảng sau?
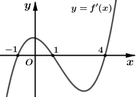
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Cho hàm số y= f( x) có đạo hàm là hàm số y= f’(x) trên R. Biết rằng hàm số y= f’ ( x-2) + 2 có đồ thị như hình vẽ bên dưới. Hàm số y= f( x) nghịch biến trên khoảng nào?
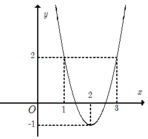
A. ![]() .
.
B. (- 1; 1)
C. ![]() .
.
D. ![]() .
.
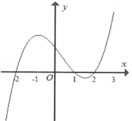
Cho hàm số y=f(x) liên tục và có đạo hàm trên R đồ thị hàm số y=f'(x) như hình vẽ bên dưới. Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
![]()
![]()
![]()
![]()