đạt cực đại tại
Các câu hỏi tương tự
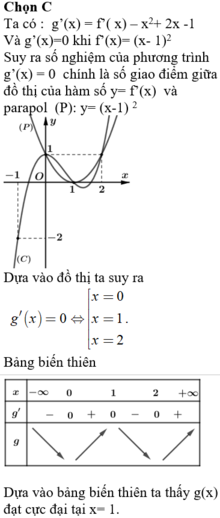
Cho hàm số y= f( x) có đạo hàm trên R. Đồ thị hàm số y= f’(x) như hình vẽ bên dưới. Hàm số g(x) = 2f(x) + x2 đạt cực tiểu tại điểm
A . x=-1
B. x= 0
C . x= 1
D.x= 2
Cho hàm số yf(x) có đạo hàm liên tục trên R và có đồ thị hàm số yf (x) như hình vẽ bên dưới. Xét hàm số g(x)f(x^2-3) và các mệnh đề sau: I. Hàm số có 3 điểm cực trị. II. Hàm số g(x)đạt cực tiểu tại x0 III. Hàm số g(x) đạt cực đại tại x2 IV. Hàm số g(x) đồng biến trên khoảng (-2;0) V. Hàm số g(x) nghịch biến trên khoảng (-1;1) Có bao nhiêu mệnh đề đúng trong các mệnh đề trên? A.1 B.4 C.3 D.2
Đọc tiếp
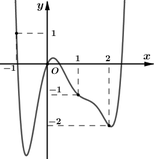
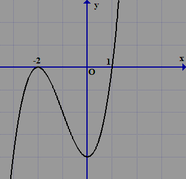
Cho hàm số y=f(x) có đạo hàm liên tục trên R và có đồ thị hàm số y=f '(x) như hình vẽ bên dưới. Xét hàm số g(x)=f(x^2-3) và các mệnh đề sau:
I. Hàm số 
có 3 điểm cực trị.
II. Hàm số g(x)đạt cực tiểu tại x=0
III. Hàm số g(x) đạt cực đại tại x=2
IV. Hàm số g(x) đồng biến trên khoảng (-2;0)
V. Hàm số g(x) nghịch biến trên khoảng (-1;1)
Có bao nhiêu mệnh đề đúng trong các mệnh đề trên?
A.1
B.4
C.3
D.2
Cho hàm số y f(x) có đạo hàm trên R và đồ thị hình bên dưới là đồ thị của đạo hàm số : y f’(x) . Hàm số y g(x) f(x) + x đạt cực tiểu tại điểm A. x 0 B.x 1 C. x 2 D. Không có điểm cực tiểu
Đọc tiếp
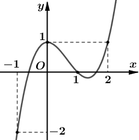
Cho hàm số y= f(x) có đạo hàm trên R và đồ thị hình bên dưới là đồ thị của đạo hàm số : y= f’(x) . Hàm số y= g(x) = f(x) + x đạt cực tiểu tại điểm
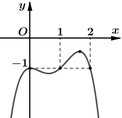
A. x= 0
B.x= 1
C. x= 2
D. Không có điểm cực tiểu
Cho hàm số y f(x) . Biết f(x) có đạo hàm f’(x) và hàm số y f’(x) có đồ thị như hình vẽ. Hàm số g( x) f(x- 1) đạt cực đại tại điểm nào dưới đây? A. x 2 B. x 4 C . x 3 D. x 1
Đọc tiếp
Cho hàm số y= f(x) . Biết f(x) có đạo hàm f’(x) và hàm số y= f’(x) có đồ thị như hình vẽ.
Hàm số g( x) = f(x- 1) đạt cực đại tại điểm nào dưới đây?
A. x= 2
B. x= 4
C . x= 3
D. x= 1
Cho hàm số f(x) có đạo hàm cấp hai f(x) liên tục trên R và có đồ thị hàm số f(x) như hình vẽ bên. Biết rằng hàm số f(x) đạt cực đại tại điểm x 1 đường thẳng trong hình vẽ bên là tiếp tuyến của đồ thị hàm số f(x) tại điểm có hoành độ x 2 . Tích phân
∫
0
ln
3
e
x
f
e...
Đọc tiếp
Cho hàm số f(x) có đạo hàm cấp hai f''(x) liên tục trên R và có đồ thị hàm số f(x) như hình vẽ bên. Biết rằng hàm số f(x) đạt cực đại tại điểm x = 1 đường thẳng 
trong hình vẽ bên là tiếp tuyến của đồ thị hàm số f(x) tại điểm có hoành độ x = 2 . Tích phân
∫
0
ln
3
e
x
f
"
e
x
+
1
2
d
x
bằng
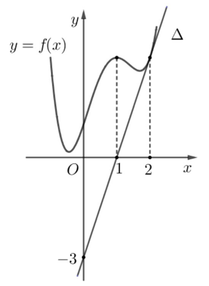
A. 8
B. 4
C. 3
D. 6
Cho hàm số f(x) có đạo hàm cấp hai f(x) liên tục trên R và đồ thị hàm số f(x) như hình vẽ bên. Biết rằng hàm số f(x) đạt cực đại tại điểm x1; đường thẳng
∆
trong hình vẽ bên là tiếp tuyến của đồ thị hàm số f(x) tại điểm có hoành độ x2. Tích phân
∫
0
ln
3
e
x
f
(
e
x...
Đọc tiếp
Cho hàm số f(x) có đạo hàm cấp hai f'''(x) liên tục trên R và đồ thị hàm số f(x) như hình vẽ bên. Biết rằng hàm số f(x) đạt cực đại tại điểm x=1; đường thẳng ∆ trong hình vẽ bên là tiếp tuyến của đồ thị hàm số f(x) tại điểm có hoành độ x=2. Tích phân ∫ 0 ln 3 e x f ' ' ( e x + 1 2 ) d x bằng
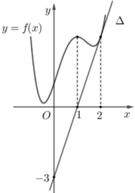
A. 8
B. 4
C. 3
D. 6
Cho hàm số y = f(x) có đạo hàm trên R. Đồ thị hàm số y= f’(x) như hình vẽ bên dưới
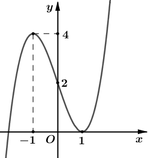
Số điểm cực trị của hàm số y= g( x)= f( x- 2017) – 2018x+ 2019 là
A. 1
B. 2
C.3
D. 4
Cho hàm số y f( x) có đạo hàm là hàm số y f’(x) trên R. Biết rằng hàm số y f’ ( x-2) + 2 có đồ thị như hình vẽ bên dưới. Hàm số y f( x) nghịch biến trên khoảng nào? A. . B. (- 1; 1) C. . D. .
Đọc tiếp
Cho hàm số y= f( x) có đạo hàm là hàm số y= f’(x) trên R. Biết rằng hàm số y= f’ ( x-2) + 2 có đồ thị như hình vẽ bên dưới. Hàm số y= f( x) nghịch biến trên khoảng nào?
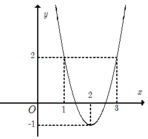
A. 
.
B. (- 1; 1)
C. 
.
D. 
.
Cho hàm số y f (x) có đạo hàm trên
ℝ
. Biết hàm số
y
f
x
có đồ thị như hình vẽ. Hàm số g (x) f (x) + x đạt cực tiểu tại điểm A. x 1 B. x 2 C.Không có điểm cực tiểu D. x 0
Đọc tiếp
Cho hàm số y = f (x) có đạo hàm trên ℝ . Biết hàm số y = f ' x có đồ thị như hình vẽ. Hàm số g (x) = f (x) + x đạt cực tiểu tại điểm
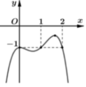
A. x = 1
B. x = 2
C.Không có điểm cực tiểu
D. x = 0