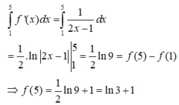Các câu hỏi tương tự
Biết hàm số f(x) có đạo hàm f’(x) liên tục trên R và f(1) e2,
∫
1
ln
3
f
x
d
x
9
-
e
2
. Tính f(ln3). A. f(ln3) ln3 + 2e2 B. f(ln3) 3 C. f(ln3) 9 – 2e2 D. f(ln3) 9
Đọc tiếp
Biết hàm số f(x) có đạo hàm f’(x) liên tục trên R và f(1) = e2, ∫ 1 ln 3 f ' x d x = 9 - e 2 . Tính f(ln3).
A. f(ln3) = ln3 + 2e2
B. f(ln3) = 3
C. f(ln3) = 9 – 2e2
D. f(ln3) = 9
Biết hàm số f(x) có đạo hàm f(x) liên tục trên
ℝ
và f(1)
e
2
,
∫
1
ln
2
f
(
x
)
d
x
4
-
e
2
Tính f(ln2).
Đọc tiếp
Biết hàm số f(x) có đạo hàm f'(x) liên tục trên ℝ và f(1)= e 2 , ∫ 1 ln 2 f ' ( x ) d x = 4 - e 2 Tính f(ln2).
![]()
![]()
![]()
Cho f(x) là hàm số bậc 4 thỏa mãn fleft(0right)dfrac{-1}{ln2}. Hàm số fleft(xright) có bảng biến thiên như sau: Hàm số gleft(xright)left|fleft(-x^2right)-x^2+dfrac{2^{x^2}}{ln2}right| có bao nhiêu điểm cực trị?A. 3B.2C.4D.5
Đọc tiếp
Cho f(x) là hàm số bậc 4 thỏa mãn \(f\left(0\right)=\dfrac{-1}{\ln2}\). Hàm số \(f'\left(x\right)\) có bảng biến thiên như sau:
Hàm số \(g\left(x\right)=\left|f\left(-x^2\right)-x^2+\dfrac{2^{x^2}}{\ln2}\right|\) có bao nhiêu điểm cực trị?
A. 3
B.2
C.4
D.5
Cho hàm số y f(x) có đạo hàm liên tục trên [1;2] thỏa mãn
∫
1
2
f
(
x
)
d
x
10
và
∫
1
2
f
(
x
)
f
(
x
)...
Đọc tiếp
Cho hàm số y = f(x) có đạo hàm liên tục trên [1;2] thỏa mãn ∫ 1 2 f ' ( x ) d x = 10 và ∫ 1 2 f ' ( x ) f ( x ) d x = ln 2 . Biết rằng f(x)>0. Tính f(2)
A. f(2) = 10
B. f(2) = -20
C. f(2) = -10
D. f(2) = 20
Họ nguyên hàm F(x) của hàm số
f
(
x
)
2
-
ln
2
(
2
x
+
1
)
2
x
+
1
Đọc tiếp
Họ nguyên hàm F(x) của hàm số f ( x ) = 2 - ln 2 ( 2 x + 1 ) 2 x + 1
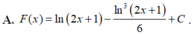
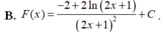
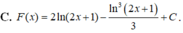
![]()
Cho hàm số yf(x) có đạo hàm là
f
(
x
)
1
2
x
-
1
và f(1)1 thì f(5) có giá trị là
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm là f ' ( x ) = 1 2 x - 1 và f(1)=1 thì f(5) có giá trị là
![]()
![]()
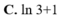
![]()
Cho hàm số
y
f
(
x
)
có đạo hàm là
f
x
1
2
x
-
1
và
f
(
1
)
1
.
G
i
á
t
r
ị
f
(
5
)
A....
Đọc tiếp
Cho hàm số y = f ( x ) có đạo hàm là f ' x = 1 2 x - 1 và f ( 1 ) = 1 . G i á t r ị f ( 5 )
A. 1 + ln3
B. ln2
C. 1 + ln2
D. ln3
Cho hàm số y f(x) có đạo hàm f’(x) liên tục trên đoạn [1; 4], f(1) 12 và
∫
1
4
f
(
x
)
d
x
17
.Giá trị của f(4) bằng A. 29 B. 5 C. 19 D. 9
Đọc tiếp
Cho hàm số y = f(x) có đạo hàm f’(x) liên tục trên đoạn [1; 4], f(1) = 12 và ∫ 1 4 f ' ( x ) d x = 17 .Giá trị của f(4) bằng
A. 29
B. 5
C. 19
D. 9
Cho hàm số f(x) có đạo hàm là f(x). Đồ thị của hàm số y f(x) được cho như hình vẽ dưới đây: Biết rằng f(-1) + f(0) f(1) + f(2). Giá trị nhỏ nhất và giá trị lớn nhất của hàm số y f(x) trên đoạn [-1;2] lần lượt là: A. f(1);f(2) B. f(2);f(0) C. f(0);f(2) D. f(1);f(-1)
Đọc tiếp
Cho hàm số f(x) có đạo hàm là f'(x). Đồ thị của hàm số y = f'(x) được cho như hình vẽ dưới đây:
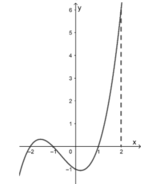
Biết rằng f(-1) + f(0) < f(1) + f(2). Giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = f(x) trên đoạn [-1;2] lần lượt là:
A. f(1);f(2)
B. f(2);f(0)
C. f(0);f(2)
D. f(1);f(-1)