Chọn đáp án A.
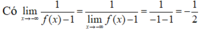
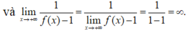
Vì vậy y = - 1 2 là tiệm cận ngang duy nhất.
Vì lim x → ∞ 1 f x - 1 = ∞ ⇒ x = 0 là tiệm đứng duy nhất
Chọn đáp án A.
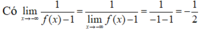
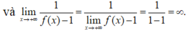
Vì vậy y = - 1 2 là tiệm cận ngang duy nhất.
Vì lim x → ∞ 1 f x - 1 = ∞ ⇒ x = 0 là tiệm đứng duy nhất
Cho hàm số
y
=
f
(
x
)
=
a
x
4
+
b
x
2
+
c
có đồ thị như hình bên dưới. Tìm tổng tất cả các đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
y
=
x
(
x
-
1
)
f
(
x
)
-
1
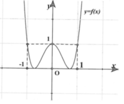
![]()
![]()
![]()
![]()
Xét các khẳng định sau:
(1) Nếu hàm số y=f(x) xác định trên R thỏa mãn f(-1).f(0)<0 thì đồ thị của hàm số y=f(x) và trục hoành có ít nhất 1 điểm chung.
(2) Nếu hàm số y=f(x) xác định trên R thỏa mãn f(-1).f(0)<0 và f(0).f(1)<0 thì đồ thị của hàm số y=f(x) và trục hoành có ít nhất 2 điểm chung.
Phát biểu nào sau đây đúng?
A. Khẳng định ![]() đúng và khẳng định
đúng và khẳng định ![]() sai.
sai.
B. Khẳng định ![]() sai và khẳng định
sai và khẳng định ![]() đúng.
đúng.
C. Khẳng định ![]() sai và khẳng định
sai và khẳng định ![]() sai.
sai.
D. Khẳng định ![]() đúng và khẳng định
đúng và khẳng định ![]() đúng.
đúng.
Cho các mệnh đề sau
(1) Đường thẳng y = y 0 là đường tiệm cận ngang của đồ thị hàm số y = f(x) nếu lim x → x 0 f x = y 0 h o ặ c lim x → x 0 f x = y 0
(2) Đường thẳng y = y 0 là đường tiệm cận ngang của đồ thị hàm số y = f(x) nếu lim x → - ∞ f x = y 0 h o ặ c lim x → + ∞ f x = y 0
(3) Đường thẳng x = x 0 là đường tiệm cận đứng của đồ thị hàm số y = f(x) nếu lim x → x 0 + f x = + ∞ h o ặ c lim x → x 0 - f x = - ∞
(4) Đường thẳng x = x 0 là đường tiệm cận đứng của đồ thị hàm số y = f(x) nếu lim x → x 0 + f x = - ∞ h o ặ c lim x → x 0 - f x = - ∞
Trong các mệnh đề trên, số mệnh đề đúng là:
A. 1
B. 2
C. 3
D. 4
Hàm số y = f(x) có bảng biến thiên dưới đây
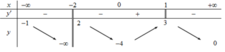
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y = f(x) là
A. 2.
B. 4.
C. 1.
D. 3.
Cho hàm số y = f(x) xác định và có đạo hàm trên R \ ± 1 . Hàm số có bảng biến thiên như hình vẽ dưới đây. Hỏi đồ thị hàm số y = f(x) có tất cả bao nhiêu đường tiệm cận?
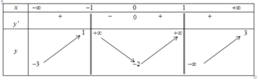
A. 1.
B. 2.
C. 3.
D. 4.
Cho hàm số y = f ( x ) có bảng biến thiên như hình dưới đây.
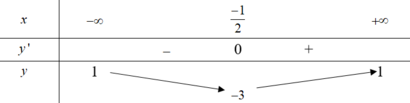
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số y = 1 2 f x - 1 là
A. 0
B. 1
C. 2
D. 3
Hàm số y = f(x) có đạo hàm trên R \ { -2; 2}, có bảng biến thiên như sau:
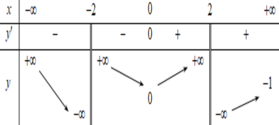
Gọi k, l lần lượt là số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y = 1 f ( x ) - 2018 . Tính k + l
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Cho hàm số y = f(x) có bảng biến thiên sau:
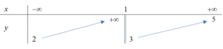
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là
A. 4.
B. 1.
C. 3.
D. 2.
Cho hàm số y = f(x) có bảng biến thiên như sau
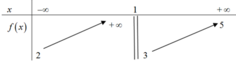
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là
A. 4.
B. 1.
C. 3.
D. 2.