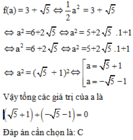Các câu hỏi tương tự
Cho hàm số y = f(x) = -2 x 2 . Tổng các giá trị a của thỏa mãn f(a) = - 8 + 4 3 là:
A. 1
B. 0
C. 10
D. -10
a) Cho hàm số
y
f
(
x
)
2
3
x
Tính: f(-2); f(-1); f(0); f(1/2); f(1); f(2); f(3)b) Cho hàm số
y
g
(
x
)
2
3
x
+
3
Tính: g(-2); g(-1); g(0); g(1/2); g(1); g(2); g(3)c) Có nhận xét gì về giá trị của hai hàm số đã cho ở trên khi biến x lấy cùng một giá trị?
Đọc tiếp
a) Cho hàm số
y = f ( x ) = 2 3 x
Tính: f(-2); f(-1); f(0); f(1/2); f(1); f(2); f(3)
b) Cho hàm số
y = g ( x ) = 2 3 x + 3
Tính: g(-2); g(-1); g(0); g(1/2); g(1); g(2); g(3)
c) Có nhận xét gì về giá trị của hai hàm số đã cho ở trên khi biến x lấy cùng một giá trị?
Cho hàm số
y
f
(
x
)
−
2
x
2
. Tổng các giá trị của a thỏa mãn
f
(
a
)
−
8
+
4
3
A. 1 B. 0 C. 10 D. −10
Đọc tiếp
Cho hàm số y = f ( x ) = − 2 x 2 . Tổng các giá trị của a thỏa mãn f ( a ) = − 8 + 4 3
A. 1
B. 0
C. 10
D. −10
Cho hàm số y = f ( x ) = - 2 x 2 . Tổng các giá trị của a thỏa mãn f(a) = -8 + 4 3 là:
A. 1
B. 0
C. 10
D. 2
bài 1 cho hàm số bặc nhất yf(x) ax +3 (a khác 0)1) tìm hệ số góc a , biết rằng đồ thị của hàm số // với đường thẳng y3/2x2) với hệ số a vừa tìm được a) hàm số trên là đồng biến hay nghịch biến trên R b) Hãy tính f(0); f(-1)c tìm giá trị của m để hàm số đồ thị y(m-5/2)x+1 // với đồ thji hàm số trênbài 2 :cho 2 đường thẳng y(k-3)x-3k+3(d1) và y (2k+1)x+k5(d2) tìm các giá trị của k đểa ) d1 và d2 cát nhau b) s1 và d2 cắt nhau tạ 1 điểm trên trjuc tung c) d1 và d2 // với nhau d) d1 và d2 vương g...
Đọc tiếp
bài 1 cho hàm số bặc nhất y=f(x) =ax +3 (a khác 0)
1) tìm hệ số góc a , biết rằng đồ thị của hàm số // với đường thẳng y=3/2x
2) với hệ số a vừa tìm được
a) hàm số trên là đồng biến hay nghịch biến trên R
b) Hãy tính f(0); f(-1)
c tìm giá trị của m để hàm số đồ thị y=(m-5/2)x+1 // với đồ thji hàm số trên
bài 2 :cho 2 đường thẳng y=(k-3)x-3k+3(d1) và y= (2k+1)x+k=5(d2) tìm các giá trị của k để
a ) d1 và d2 cát nhau
b) s1 và d2 cắt nhau tạ 1 điểm trên trjuc tung
c) d1 và d2 // với nhau
d) d1 và d2 vương góc với nhau
e) d1 và d2 trùng nhau
Cho hàm số y = f(x) = 1/2x + 5
a) Biểu diễn các điểm sau trên mặt phẳng tọa độ Oxy:
A(1/3; 6), B(1/2; 4), C(1; 2), D(2; 1), E(3; 2/3), F(4; 1/2).
b) Vẽ đồ thị của hàm số y = 2x.
Cho đa thức f(x) bậc 4 , hệ số của bậc cao nhất là 1 và thỏa mãn :f(1)=3 ; f(3) =11 ; f(5)=27 . Tính giá trị A= f(-2) + 7f(6) = ?
a) Cho các số a,b thỏa mãn: a2+b2=a3+b3=1
Tính giá trị biểu thức: A=a4+b4
b) Cho số tự nhiên a và số nguyên tố p thỏa mãn đẳng thức: a3=2p+1
Tìm a và p
c) Cho đa thức f(x),tìm dư của phép chia f(x) cho (x-1)(x+2).Biết rằng f(x) chia cho x-1 dư 7 và f(x) chia cho x+2 dư 1.
Bạn nào biết giúp mik vs nhé!!!!
Bài 1: Cho các số thực dương a,b,c thỏa mãn các điều kiện left(a+cright)left(b+cright)4c^2. Tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thứcPfrac{a}{b+3c}+frac{b}{a+3c}+frac{ab}{bc+ca}Bài 2: Cho x,y,z thỏa mãn x+y+z0 và x^2+y^2+z^21. Tìm GTLN của biểu thức Px^5+y^5+z^5Bài 3: Cho a,b,c dương thỏa mãn a+b+c1.Tìm Min P2020left(frac{a^2}{b}+frac{b^2}{c}+frac{c^2}{a}right)+frac{1}{3left(a^2+b^2+c^2right)}Bài 4: Cho a,b,c là các số thực không âm thỏa mãn điều kiện a+b+c3. Tìm GTLN của biểu thức Pa...
Đọc tiếp
Bài 1: Cho các số thực dương a,b,c thỏa mãn các điều kiện \(\left(a+c\right)\left(b+c\right)=4c^2\). Tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức
\(P=\frac{a}{b+3c}+\frac{b}{a+3c}+\frac{ab}{bc+ca}\)
Bài 2: Cho x,y,z thỏa mãn x+y+z=0 và \(x^2+y^2+z^2=1\). Tìm GTLN của biểu thức \(P=x^5+y^5+z^5\)
Bài 3: Cho a,b,c dương thỏa mãn \(a+b+c=1.\)Tìm Min
\(P=2020\left(\frac{a^2}{b}+\frac{b^2}{c}+\frac{c^2}{a}\right)+\frac{1}{3\left(a^2+b^2+c^2\right)}\)
Bài 4: Cho a,b,c là các số thực không âm thỏa mãn điều kiện a+b+c=3. Tìm GTLN của biểu thức \(P=a\sqrt{b^3+1}+b\sqrt{c^3+1}+c\sqrt{a^3+1}\)