Các câu hỏi tương tự
Cho hàm số yf(x) có đạo hàm liên tục trên R và có đồ thị hàm số yf (x) như hình vẽ bên dưới. Xét hàm số g(x)f(x^2-3) và các mệnh đề sau: I. Hàm số có 3 điểm cực trị. II. Hàm số g(x)đạt cực tiểu tại x0 III. Hàm số g(x) đạt cực đại tại x2 IV. Hàm số g(x) đồng biến trên khoảng (-2;0) V. Hàm số g(x) nghịch biến trên khoảng (-1;1) Có bao nhiêu mệnh đề đúng trong các mệnh đề trên? A.1 B.4 C.3 D.2
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm liên tục trên R và có đồ thị hàm số y=f '(x) như hình vẽ bên dưới. Xét hàm số g(x)=f(x^2-3) và các mệnh đề sau:
I. Hàm số 
có 3 điểm cực trị.
II. Hàm số g(x)đạt cực tiểu tại x=0
III. Hàm số g(x) đạt cực đại tại x=2
IV. Hàm số g(x) đồng biến trên khoảng (-2;0)
V. Hàm số g(x) nghịch biến trên khoảng (-1;1)
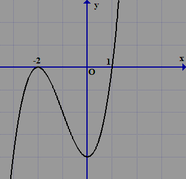
Có bao nhiêu mệnh đề đúng trong các mệnh đề trên?
A.1
B.4
C.3
D.2
Xét các khẳng định sau i) Nếu hàm số yf(x) có đạo hàm cấp hai trên R và đạt cực tiểu tại
x
x
0
thì
f
x
0
0
f...
Đọc tiếp
Xét các khẳng định sau
i) Nếu hàm số y=f(x) có đạo hàm cấp hai trên R và đạt cực tiểu tại x = x 0 thì f ' x 0 = 0 f ' ' x 0 > 0
ii) Nếu hàm số y=f(x) có đạo hàm cấp hai trên R và đạt cực đại tại x = x 0 thì f ' x 0 = 0 f ' ' x 0 < 0
iii) Nếu hàm số y=f(x) có đạo hàm cấp hai trên R và f ' ' x 0 = 0 thì hàm số không đạt cực trị tại x = x 0
Số khẳng định đúng trong các khẳng định trên là
A. 0
B. 1
C. 2
D. 3
Cho hàm số: y = –( m 2 + 5m) x 3 + 6m x 2 + 6x – 5
a) Xác định m để hàm số đơn điệu trên R. Khi đó, hàm số đồng biến hay nghịch biến? Tại sao?
b) Với giá trị nào của m thì hàm số đạt cực đại tại x = 1 ?
16 tháng 12 2021 lúc 19:51
cho hàm số y= x3. Khẳng định nào sau đây đúng?
A. Hàm số nghịch biến trên \(R\)
B. Hàm số đồng biến trên \(R\)
C. Hàm số đồng biến trên (-∞;0)
D. Hàm số nghịch biến trên (0;+∞)
chỉ mik cách lập nhóm nhaTrích một số bài toán trong đề:+ Trên mặt phẳng phức, tập hợp điểm biểu diễn cho số phức z thỏa mãn điều kiện /z/ 2 là:A. Đường tròn tâm O, bán kính R 2B. Đường tròn tâm O, bán kính R 4C. Đường tròn tâm O, bán kính R 1/2D. Đường tròn tâm O , bán kính R căn 2+ Cho hàm số y f(x) xác định, liên tục trên R và có bảng biến thiên như hình vẽ. Khẳng định nào sau đây đúng?A. Hàm số y f(x) có giá trị cực đại bằng 0B. Giá trị lớn nhất của hàm số y f(x) trên tập R là 1C. Hà...
Đọc tiếp
chỉ mik cách lập nhóm nha
Trích một số bài toán trong đề:
+ Trên mặt phẳng phức, tập hợp điểm biểu diễn cho số phức z thỏa mãn điều kiện /z/ = 2 là:
A. Đường tròn tâm O, bán kính R = 2
B. Đường tròn tâm O, bán kính R = 4
C. Đường tròn tâm O, bán kính R = 1/2
D. Đường tròn tâm O , bán kính R = căn 2
+ Cho hàm số y = f(x) xác định, liên tục trên R và có bảng biến thiên như hình vẽ. Khẳng định nào sau đây đúng?
A. Hàm số y = f(x) có giá trị cực đại bằng 0
B. Giá trị lớn nhất của hàm số y = f(x) trên tập R là 1
C. Hàm số y = f(x) đạt cực đại tại x = 0 và cực tiểu tại x = -1
D. Hàm số y = f(x) có đúng một cực trị
+ Tìm phần thực của số phức (2 + 3i).i^10
Cho các phát biểu sau: I. Đồ thị hàm số có y x4 – x + 2 có trục đối xứng là Oy. II. Hàm số f(x) liên tục và có đạo hàm trên khoảng (a;b) đạt cực trị tại điểm x0 thuộc khoảng (a;b) thì tiếp tuyến tại điểm M(x0,f(x0)) song song với trục hoành. III. Nếu f(x) nghịch biến trên khoảng (a;b) thì hàm số không có cực trị trên khoảng (a;b). IV. Hàm số f(x) xác định và liên tục trên khoảng (a;b) và đạt cực tiểu tại điểm x0 thuộc khoảng (a;b) thì f(x) nghịch biến trên khoảng (a;x0) và đồng biến trên khoảng...
Đọc tiếp
Cho các phát biểu sau:
I. Đồ thị hàm số có y = x4 – x + 2 có trục đối xứng là Oy.
II. Hàm số f(x) liên tục và có đạo hàm trên khoảng (a;b) đạt cực trị tại điểm x0 thuộc khoảng (a;b) thì tiếp tuyến tại điểm M(x0,f(x0)) song song với trục hoành.
III. Nếu f(x) nghịch biến trên khoảng (a;b) thì hàm số không có cực trị trên khoảng (a;b).
IV. Hàm số f(x) xác định và liên tục trên khoảng (a;b) và đạt cực tiểu tại điểm x0 thuộc khoảng (a;b) thì f(x) nghịch biến trên khoảng (a;x0) và đồng biến trên khoảng (x0;b).
Các phát biểu đúng là:
A. II,III,IV
B. I,II,III
C. III,IV
D. I,III,IV
Cho hàm số
y
f
(
x
)
xác định trên R, có bảng biến thiên như sau. Hàm số
y
f
(
x
)
đạt cực đại tại điểm A. x4 B. x-2 C. x-1 D. x3
Đọc tiếp
Cho hàm số y = f ( x ) xác định trên R, có bảng biến thiên như sau. Hàm số y = f ( x ) đạt cực đại tại điểm
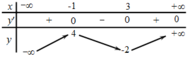
A. x=4
B. x=-2
C. x=-1
D. x=3
Khẳng định nào sau đây đúng?
A. y = sin3x là hàm số chẵn
B. Hàm số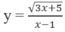 
xác định trên R
C. Hàm số y = x 3 + 4x - 5 đồng biến trên R
D. Hàm số y = sinx + 3x - 1 nghịch biến trên R
Cho hàm số y=f(x) liên tục trên R và có bảng biến thiên như sau:
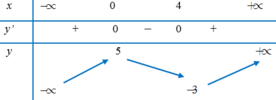
Hàm số đạt cực đại tại điểm nào trong các điểm dưới đây?
A. x = -3
B. x = 5
C. x = 4
D. x = 0
Khẳng định nào sau đây đúng?A. y sin3x là hàm số chẵnB. Hàm số
y
3
x
+
5
x
-
1
xác định trên RC. Hàm số y
x
3
+ 4x - 5 đồng biến trên RD. Hàm số y sinx + 3x - 1 nghịc...
Đọc tiếp
Khẳng định nào sau đây đúng?
A. y = sin3x là hàm số chẵn
B. Hàm số y = 3 x + 5 x - 1 xác định trên R
C. Hàm số y = x 3 + 4x - 5 đồng biến trên R
D. Hàm số y = sinx + 3x - 1 nghịch biến trên R