Ta có
y ' = x 2 + 2 x ; y ' ' = 2 x + 2 ⇒ y ' ' = 0 ⇔ x = - 1 ⇔ - 4 / 3 , y ' ( - 1 ) = - 1
Phương trình tiếp tuyến của đồ thị hàm số tại điểm x = -1 là:
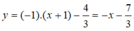
Chọn đáp án A.
Ta có
y ' = x 2 + 2 x ; y ' ' = 2 x + 2 ⇒ y ' ' = 0 ⇔ x = - 1 ⇔ - 4 / 3 , y ' ( - 1 ) = - 1
Phương trình tiếp tuyến của đồ thị hàm số tại điểm x = -1 là:
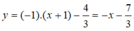
Chọn đáp án A.
Cho hàm số y = f(x) = a x + b c x + d ( a,b,c,d ∈ ℝ , - d c ≠ 0) đồ thị hàm số y= f’(x) như hình vẽ.

Biết đồ thị hàm số y= f(x) cắt trục tung tại điểm có tung độ bằng 3. Tìm phương trình tiếp tuyến của (C) tại giao điểm của (C) với trục hoành ?
A. y = x - 3 x + 1
B. y = x + 3 x - 1
C. y = x + 3 x + 1
D. y = x - 3 x - 1
Phương trình tiếp tuyến của đồ thị hàm số y = x - 1 x + 2 tại điểm có hoành độ bằng -3 là:
A. y = 3 x + 13
B. y = - 3 x - 5
C. y = 3 x + 5
D. y = - 3 x + 13
Phương trình tiếp tuyến của đồ thị hàm số y = x 4 - 2 x 2 tại điểm có hoành độ x = -2 là:
A. y = -24x + 40 B. y = 24x - 40
C. y = -24x - 40 D. y = -24x
Phương trình tiếp tuyến của đồ thị hàm số y = x 4 - 2 x 2 tại điểm có hoành độ x = -2 là:
A. y = -24x + 40 B. y = 24x - 40
C. y = -24x - 40 D. y = -24x
Viết phương trình tiếp tuyến của đồ thị hàm số:
\(y=x^3-6x+5\)
a, Tại điểm có hoành độ \(x_0=1\)
b, Tại điểm có tung độ \(y_0=5\)
c, Hệ số góc \(k=-9\)
Cho hàm số y = x + 2 2 x + 3 có đồ thị (C). Đường thẳng d có phương trình y = a x + b là tiếp tuyến của (C), biết d cắt trục hoành tại A và cắt trục tung tại B sao cho tam giác OAB cân tại O, với O là gốc tọa độ. Tính a+b
A. -1
B. -2
C. 0
D. -3
Cho hàm số y = x + 2 2 x + 3 có đồ thị (C). Đường thẳng (d) có phương trình y = a x + b là tiếp tuyến của (C), biết (d) cắt trục hoành tại A và cắt trục tung tại B sao cho tam giác OAB cân tại O, với O là gốc tọa độ. Tính a + b
A. 0
B. -2
C. -1
D. -3
Cho hàm số y= f(x) có đạo hàm liên tục trên R, thỏa mãn 2 f ( 2 x ) + f ( 1 - 2 x ) = 12 x 3 . Tìm phương trình tiếp tuyến của đồ thị hàm số y = f(x) tại điểm có hoành độ x = 1
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Cho hàm số y = f ( x ) = a x 3 + b x 2 + c x + d ( v ớ i a , b , c , d ∈ ℝ , a > 0 ) . Biết đồ thị hàm số y=f(x) này có điểm cực đại A (0;1) và điểm cực tiểu B(2;-3). Hỏi tập nghiệm của phương trình f 3 ( x ) + f ( x ) - 2 f ( x ) 3 = 0 có bao nhiêu phần tử?
A. 2019
B. 2018
C. 9
D. 8