Chọn D
Từ giả thiết ta có:
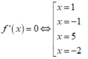
![]()
Từ bảng biến thiên ta thấy f'(x) đổi dấu tại x = -2 và x = 5 do đó hàm số f(x) có 2 điểm cực trị.
Chọn D
Từ giả thiết ta có:
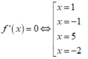
![]()
Từ bảng biến thiên ta thấy f'(x) đổi dấu tại x = -2 và x = 5 do đó hàm số f(x) có 2 điểm cực trị.
Cho hàm số \(f\left(x\right)\) có đạo hàm bằng \(f'\left(x\right)=x^2\left(x-1\right)^3\left(x-2\right)\) . Số điểm cực trị của hàm số \(f\left(x\right)\) bằng:
A.0 B.1 C.2 D.3
Cho hàm số y= f( x) có đạo hàm f ' ( x ) = ( x + 1 ) 4 ( x - 2 ) 5 ( x + 3 ) 3 Số điểm cực trị của hàm số f x là
A. 5
B. 3
C. 1
D. 2
Cho hàm số y = f ( x ) có đạo hàm f ' ( x ) = ( x + 1 ) ( x - 2 ) 2 ( x - 3 ) 3 ( x + 5 ) 4 . Hỏi hàm số y = f ( x ) có mấy điểm cực trị?
A. 2
B. 3
C. 4
D. 5
Cho hàm số f(x) có đạo hàm f ' ( x ) = x 2 ( x - 1 ) 3 ( x - 2 ) 4 ( x - 3 ) 5 , ∀ x ∈ ℝ . Số điểm cực trị của hàm số đã cho là
A. 1
B. 4
C. 2
D. 3
Cho hàm số f có đạo hàm là f ' ( x ) = x ( x + 1 ) 2 ( x - 2 ) 4 với mọi x ∈ R. Số điểm cực trị của hàm số f là:
A. 0
B. 1
C. 2
D. 3
Cho hàm số f(x) có đạo hàm là f ' ( x ) = x ( x + 1 ) 2 ( x - 2 ) 4 với mọi x ∈ ℝ . Số điểm cực trị của hàm số f(x) là
A. 0
B. 3
C. 2
D. 1
Cho f ( x ) có đạo hàm f ' ( x ) = x ( x + 1 ) 3 ( x - 2 ) 2 . Số điểm cực trị của hàm số f ( x ) là
A. 1
B. 2
C. 3
D. 6
Cho hàm số y = f ( x ) có đạo hàm f ' ( x ) = x 2 ( x - 1 ) ( x - 2 ) ( 3 x - 1 ) , ∀ x ∈ ℝ . Số điểm cực trị của hàm số đã cho bằng
A. 2
B. 1
C. 3
D. 4
Cho hàm số y = f ( x ) có đạo hàm f ' ( x ) = x ( x - 1 ) ( x + 2 ) 3 ( x - 2 ) 2 , ∀ x ∈ ℝ . Số điểm cực trị của hàm số đã cho là
A. 4
B. 7
C. 3
D. 2