Các câu hỏi tương tự
Cho hàm số f(x)=x^2-4x+3. Có bao nhieu giá trị nguyên của tham số m để phương trình f^2(/x/)-(m-6)f(/x/)-m+5=0 có 6 nghiệm phân biệt
Cho hàm số y = f(x) liên tục trên R sao cho maxf(x) = f(2) = bằng 84 trên [0; 10] . Xét hàm số g(x) = f(x3+x) - x2 + 2x + m.Tìm m để giá trị lớn nhất của g(x) trên [0; 2]
Cho hàm số f(x), g(x) có đồ thị như hình vẽ. Đặt
h
(
x
)
f
(
x
)
g
(
x
)
. Tính h(2) đạo hàm của hàm số h(x) tại x 2. A. 4/49 B. -4/49 C. 2/7 D. -2/7
Đọc tiếp
Cho hàm số f(x), g(x) có đồ thị như hình vẽ. Đặt h ( x ) = f ( x ) g ( x ) . Tính h'(2) đạo hàm của hàm số h(x) tại x = 2.
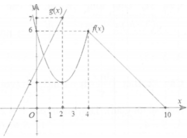
A. 4/49
B. -4/49
C. 2/7
D. -2/7
Cho hàm số yf(x) có đạo hàm trên
ℝ
. Đồ thị hàm số yf(x) như hình vẽ bên dưới Tìm m để bất phương trình
m
-
x
≥
2
f
x
+
2
+
4
x
+
3
nghiệm đúng với mọi
x
∈
-
3
;...
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm trên ℝ . Đồ thị hàm số y=f'(x) như hình vẽ bên dưới
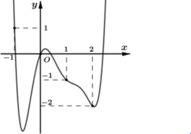
Tìm m để bất phương trình m - x ≥ 2 f x + 2 + 4 x + 3 nghiệm đúng với mọi x ∈ - 3 ; + ∞
A. m ≥ 2 f ( 0 ) - 1
B. m ≤ 2 f ( 0 ) - 1
C. m ≤ 2 f ( - 1 )
D. m ≥ 2 f ( - 1 )
Cho hàm số y = f ( x ) có đạo hàm f ' ( x ) = x ( x - 1 ) ( x + 2 ) 3 ( x - 2 ) 2 , ∀ x ∈ ℝ . Số điểm cực trị của hàm số đã cho là
A. 4
B. 7
C. 3
D. 2
Cho hàm số \(y = f(x)\) xác định trên \(R\) có đạo hàm \(f'(x)=-(x+2)(x-1)^2(x-3)\)
Số điểm cực tiểu của hàm số \(f(x^2-2x)\) là?
Cho hàm số f(x) có đạo hàm là hàm f(x). Đồ thị hàm số f(x) như hình vẽ bên. Biết rằng f(0) + f(1) - 2f(2) f(4) - f(3). Tìm giá trị nhỏ nhất m và giá trị lớn nhất M của f(x) trên đoạn [0;4]. A. m f(4), M f(2) B. m f(1), M f(2) C. m f(4), M f(1) D. m f(0), M f(2)
Đọc tiếp
Cho hàm số f(x) có đạo hàm là hàm f'(x). Đồ thị hàm số f'(x) như hình vẽ bên. Biết rằng f(0) + f(1) - 2f(2) = f(4) - f(3). Tìm giá trị nhỏ nhất m và giá trị lớn nhất M của f(x) trên đoạn [0;4].

A. m = f(4), M = f(2)
B. m = f(1), M = f(2)
C. m = f(4), M = f(1)
D. m = f(0), M = f(2)
Cho hàm số f(x) có đạo hàm trên R,
f
(
-
1
)
-
2
và
f
(
3
)
2
. Tính I
∫
-
1
3
f
(
x
)
d
x
.
Đọc tiếp
Cho hàm số f(x) có đạo hàm trên R, f ( - 1 ) = - 2 và f ( 3 ) = 2 . Tính I= ∫ - 1 3 f ' ( x ) d x .
![]()
![]()
![]()
![]()
Cho hàm số f ( x ) có f ' ( x ) = x ( x - 3 ) 2 ( x - 2 ) 3 , ∀ x ∈ ℝ . Số điểm cực tiểu của hàm số đã cho là
A. 3
B. 5
C. 1
D. 2
Cho hàm số f ( x ) có f ' ( x ) = x ( x - 3 ) 2 ( x - 2 ) 3 , ∀ x ∈ ℝ . Số điểm cực tiểu của hàm số đã cho là:
A. 3
B. 1
C. 5
D. 2