Các câu hỏi tương tự
Cho hàm số f(x) có đạo hàm không âm trên [0;1] thỏa mãn
[
f
(
x
)
]
4
.
[
f
(
x
)
]
2
(
x
2
+
1
)
1...
Đọc tiếp
Cho hàm số f(x) có đạo hàm không âm trên [0;1] thỏa mãn [ f ( x ) ] 4 . [ f ' ( x ) ] 2 ( x 2 + 1 ) = 1 + f 3 ( x ) và f(x)>0 biết f(0) = 2 Hãy chọn khẳng định đúng trong các khẳng định sau:
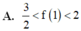
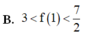
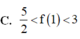
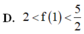
Cho hàm số
f
(
x
)
có đạo hàm
f
(
x
)
(
x
2
-
9
)
(
x
2
-
3
x
)
2
,
∀
x
∈
ℝ
. Gọi T là giá trị cực đại của hàm số đã cho. Chọn khẳng định đúng
Đọc tiếp
Cho hàm số f ( x ) có đạo hàm f ' ( x ) = ( x 2 - 9 ) ( x 2 - 3 x ) 2 , ∀ x ∈ ℝ . Gọi T là giá trị cực đại của hàm số đã cho. Chọn khẳng định đúng
![]()
![]()
![]()
![]()
Cho hàm số yf(x) thỏa mãn f(-x)f(x). Gọi đồ thị hàm số là (C). Chọn khẳng định đúng
Đọc tiếp
Cho hàm số y=f(x) thỏa mãn f(-x)=f(x). Gọi đồ thị hàm số là (C). Chọn khẳng định đúng
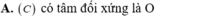
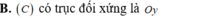
![]()
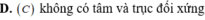
Cho hàm số yf(x), chọn khẳng định đúng? A. Nếu và thì không phải là cực trị của hàm số. B. Hàm số đạt cực trị tại khi và chỉ khi . C. Nếu hàm số có điểm cực đại và điểm cực tiểu thì giá trị cực đại lớn hơn giá trị cực tiểu. D. Nếu đổi dấu khi qua điểm và liên tục tại thì hàm số đạt cực trị tại điểm.
Đọc tiếp
Cho hàm số y=f(x), chọn khẳng định đúng?
A. Nếu ![]() và
và ![]() thì
thì ![]() không phải là cực trị của hàm số.
không phải là cực trị của hàm số.
B. Hàm số ![]() đạt cực trị tại
đạt cực trị tại ![]() khi và chỉ khi
khi và chỉ khi ![]() .
.
C. Nếu hàm số ![]() có điểm cực đại và điểm cực tiểu thì giá trị cực đại lớn hơn giá trị cực tiểu.
có điểm cực đại và điểm cực tiểu thì giá trị cực đại lớn hơn giá trị cực tiểu.
D. Nếu ![]() đổi dấu khi
đổi dấu khi ![]() qua điểm
qua điểm ![]() và
và ![]() liên tục tại
liên tục tại ![]() thì hàm số
thì hàm số ![]() đạt cực trị tại điểm
đạt cực trị tại điểm![]() .
.
Cho hàm số f(x) = ln16x Chọn khẳng định đúng.
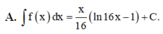
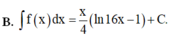
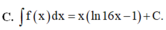
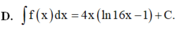
Cho hàm số y f (x) có đồ thị (C) như hình vẽ. Chọn khẳng định đúng về hàm số f (x) A. Hàm số
f
(
x
)
có điểm cực đại là
0
;
1
. B. Hàm số
f
(
x
)...
Đọc tiếp
Cho hàm số y = f (x) có đồ thị (C) như hình vẽ. Chọn khẳng định đúng về hàm số f (x)
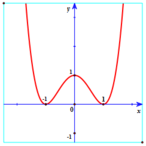
A. Hàm số f ( x ) có điểm cực đại là 0 ; 1 .
B. Hàm số f ( x ) có điểm cực tiểu là 0 ; 1 .
C. Hàm số f ( x ) có ba điểm cực trị.
D. Hàm số f ( x ) có ba giá trị cực trị.
Cho hàm số y f(x) có
lim
x
→
+
∞
f
(
x
)
0
và
lim
x
→
0
+
f
(
x
)
+
∞
. Khẳng địn...
Đọc tiếp
Cho hàm số y = f(x) có lim x → + ∞ f ( x ) = 0 và lim x → 0 + f ( x ) = + ∞ . Khẳng định nào sau đây là khẳng định đúng?
A. Đồ thị hàm số đã cho không có tiệm cận đứng
B. Trục hoành và trục tung là hai tiệm cận của đồ thị hàm số đã cho
C. Đồ thị hàm số đã cho có một tiệm cận đứng là đường thẳng y = 0
D. Hàm số đã cho có tập xác định là D = (0; +∞)
Cho hàm số yf(x) không phải là hàm hằng và
∀
x
∈
ℝ
ta có f(-x)-f(x). Gọi là đồ thị của hàm số. Chọn khẳng định đúng.
Đọc tiếp
Cho hàm số y=f(x) không phải là hàm hằng và ∀ x ∈ ℝ ta có f(-x)=-f(x). Gọi là đồ thị của hàm số. Chọn khẳng định đúng.
![]()
![]()
![]()
![]()
Cho hàm số y f(x) có
lim
x
→
0
+
f
(
x
)
-
∞
và
lim
x
→
2
+
f
(
x
)
-
∞
Khẳng định nào sau đây là khẳng định đúng? A. Đồ thị...
Đọc tiếp
Cho hàm số y = f(x) có lim x → 0 + f ( x ) = - ∞ và lim x → 2 + f ( x ) = - ∞
Khẳng định nào sau đây là khẳng định đúng?
A. Đồ thị hàm số đã cho không có tiệm cận đứng.
B. Đồ thị hàm số đã cho có đúng một tiệm cận đứng.
C. Đồ thị hàm số đã cho có hai tiệm cận đứng là các đường thẳng y = 0 và y = 2.
D. Đồ thị hàm số đã cho có hai tiệm cận đứng là các đường thẳng x = 0 và x = 2.
Cho hàm số
f
(
x
)
|
8
x
4
+
a
x
2
+
b
|
, trong đó a, b là tham số thực. Biết rằng giá trị lớn nhất của hàm số f(x) trên đoạn [-1;1] bằng 1. Hãy chọn...
Đọc tiếp
Cho hàm số f ( x ) = | 8 x 4 + a x 2 + b | , trong đó a, b là tham số thực. Biết rằng giá trị lớn nhất của hàm số f(x) trên đoạn [-1;1] bằng 1. Hãy chọn khẳng định đúng?
A. ![]() ,
, ![]()
B. ![]() ,
, ![]()
C. ![]() ,
, ![]()
D. ![]() ,
, ![]()