Chọn D
Theo định nghĩa về tính đơn điệu của hàm số, ta chọn đáp án D.
Chọn D
Theo định nghĩa về tính đơn điệu của hàm số, ta chọn đáp án D.
Cho hàm số f(x)>0 với x ∈ ℝ , f ( 0 ) = 1 và f ( x ) = x + 1 . f ' ( x ) với mọi x ∈ ℝ . Mệnh đề nào dưới đây đúng?
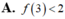
![]()
![]()
![]()
Cho hàm số f(x) liên tục trên ℝ và f(x) ≠ 0 với mọi x ∈ ℝ . f ' ( x ) = ( 2 x + 1 ) f 2 ( x ) và f(1)=-0,5. Biết rằng tổng f(1)+f(2)+f(3)+...+f(2017)= a b với a b tối giản.
Mệnh đề nào dưới đây đúng?
![]()
![]()
![]()
![]()
Cho hai số thực a, b tùy ý, F(x) là một nguyên hàm của hàm số f(x) trên tập ℝ . Mệnh đề nào dưới đây là đúng?
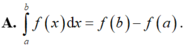
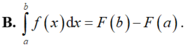
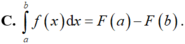
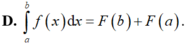
Cho hàm số f(x) có đạo hàm trên ℝ thỏa mãn f’(x) – 2018f(x) = 2018.x2017.e2018x với mọi x ∈ ℝ và f(0) = 2018. Tính giá trị f(1).
A. f(1) = 2019e2018.
B. f(1) = 2018e-2018.
C. f(1) = 2018e2018.
D. f(1) = 2017e2018.
Cho hàm số y=f(x) có đạo hàm f ' ( x ) = x x - 2 3 , với mọi x ∈ ℝ . Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A. (1;3)
B. (-1;0)
C. (0;1)
D. (-2;0)
Cho hàm số f(x) có đạo hàm là f ' ( x ) = x ( x + 1 ) 2 ( x - 2 ) 4 với mọi x ∈ ℝ . Số điểm cực trị của hàm số f(x) là
A. 0
B. 3
C. 2
D. 1
Cho hàm số y = f ( x ) xác định trên R \ { 0 } và có f ' ( x ) = 2 x 2 - x - 1 x , ∀ x ∈ ℝ . Mệnh đề nào sau đây đúng?
A. Hàm số có một điểm cực tiểu và một điểm cực đại
B. Hàm số có ba điểm cực trị
C. Hàm số có hai điểm cực tiểu
D. Hàm số có hai điểm cực đại
Cho hàm số f(x) có đạo hàm trên ℝ và f''(x) > 0, ∀ x ∈ ℝ . Biết f(1) = 2. Hỏi khẳng định nào sau đây có thể xảy ra?
A. f(2) + f(3) = 4
B. f(-1)= 2
C. f(2) = 1
D. f(2018) > f(2019)
Cho hàm số y = f ( x ) xác định trên ℝ \ 1 liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:
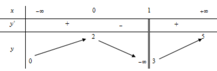
Mệnh đề nào dưới đây đúng?
A. Hàm số đạt cực đại tại x=0.
B. Giả trị cực tiểu của hàm số là y C T = 3 .
C. Giá trị cực đại của hàm số là y C D = 5 .
D. Hàm số đồng biến trên khoảng 0 ; + ∞ .
Cho hàm số f(x) liên tục trên ℝ + thỏa mãn f ' ( x ) ≥ x + 1 x và f(1) = 1 Khẳng định nào sau đây là đúng?
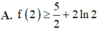
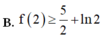
![]()
![]()