Chọn C.
![]()
![]()
![]()
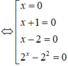
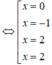
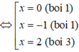
Ta thấy phương trình f ' x = 0 có 3 nghiệm phân biệt
và các nghiệm này đều là nghiệm bội lẻ nên hàm số y = f x có 3 điểm cực trị.
Chọn C.
![]()
![]()
![]()
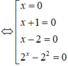
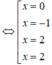
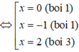
Ta thấy phương trình f ' x = 0 có 3 nghiệm phân biệt
và các nghiệm này đều là nghiệm bội lẻ nên hàm số y = f x có 3 điểm cực trị.
Cho hàm số f(x) có đạo hàm là f ' ( x ) = x ( x + 1 ) 2 ( x - 2 ) 4 với mọi x ∈ ℝ . Số điểm cực trị của hàm số f(x) là
A. 0
B. 3
C. 2
D. 1
Cho hàm số f(x) có đạo hàm f ' ( x ) = x 2 ( x - 1 ) 3 ( x - 2 ) 4 ( x - 3 ) 5 , ∀ x ∈ ℝ . Số điểm cực trị của hàm số đã cho là
A. 1
B. 4
C. 2
D. 3
Cho hàm số f ( x ) có đạo hàm f ' ( x ) = ( x 2 + x ) ( x - 2 ) 2 ( 2 x - 4 ) , ∀ x ∈ ℝ Số điểm cực trị của f ( x ) là
A. 2
B. 4
C. 3
D. 1
Cho hàm số y = f ( x ) có đạo hàm f ' ( x ) = x ( x - 1 ) ( x + 2 ) 3 ( x - 2 ) 2 , ∀ x ∈ ℝ . Số điểm cực trị của hàm số đã cho là
A. 4
B. 7
C. 3
D. 2
Cho hàm số f ( x ) có đạo hàm f ' ( x ) = ( x + 1 ) 2 ( x - 2 ) 3 ( 2 x + 3 ) , ∀ x ∈ ℝ . Số điểm cực trị của hàm số đã cho là
A. 2
B. 6
C. 1
D. 3
Cho hàm số f ( x ) có đạo hàm f ' ( x ) = x ( x - 1 ) ( x + 2 ) 3 , ∀ x ∈ ℝ . Số điểm cực trị của hàm số đã cho là:
A. 2
B. 3
C. 5
D. 1
Cho hàm số f ( x ) có đạo hàm f ' ( x ) = x ( x - 1 ) ( x - 2 ) 2 , ∀ x ∈ ℝ . Số điểm cực trị của hàm số đã cho là
A. 5
B. 2
C. 1
D. 3
Cho hàm số f ( x ) có đạo hàm f ' ( x ) = ( x - 2 ) 2 ( x - 1 ) x 3 , ∀ x ∈ ℝ . Số điểm cực trị của hàm số đã cho là
A. 0
B. 1
C. 2
D. 3
Cho hàm số f ( x ) có đạo hàm f ' ( x ) = x 3 ( x - 1 ) ( x - 2 ) , ∀ x ∈ ℝ . Số điểm cực trị của hàm số đã cho là
A. 1
B. 3
C. 2
D. 4
Cho hàm số y = f ( x ) có đạo hàm f ' ( x ) = x ( x - 1 ) ( x + 2 ) 2 , ∀ x ∈ ℝ . Tìm số điểm cực trị của hàm số đã cho
A. 3
B. 2
C. 4
D. 1